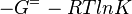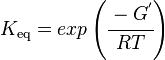Kinetic Model of Monoterpenoid Biosynthesis Wiki

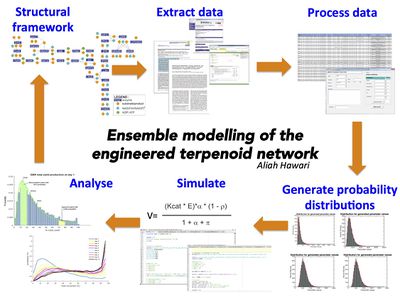
This study models the engineered monoterpene synthesis network based on all known kinetic values for each of its reaction. The general modelling approach is a modular one where each of the enzymatic reaction in the network represents an individual model and can be imagined as individual lego bricks. These lego bricks can be assembled or disassembled according to our modelling objective- either to model an individual reaction or to model a specific set of reactions to mimic our engineered constructs. Each of the enzymatic reaction is described using reversible Michaelis-Menten equation which requires various kinetic parameters such as the Michaelis-Menten constant, the turnover number and the equilibrium constant. The values for these kinetic parameters are extensively sought from published reports, enzyme and metabolic databases such as BRENDA, UniProt, ENZYME and MetaCyc, as well as from experimentally measured enzymatic assays carried out within our group. Uncertainties within the kinetic values measured from varied sources are acknowledged and is included in the modelling process. This includes incorporating generic parameter values from the BRENDA database. Our initial belief of the uncertainties associated with each kinetic parameter is represented with a lognormal probability distribution, which provides a number of plausible values to be sampled during an ensemble modelling technique. More information on uncertainty and ensemble modelling adopted for this study can be found here.

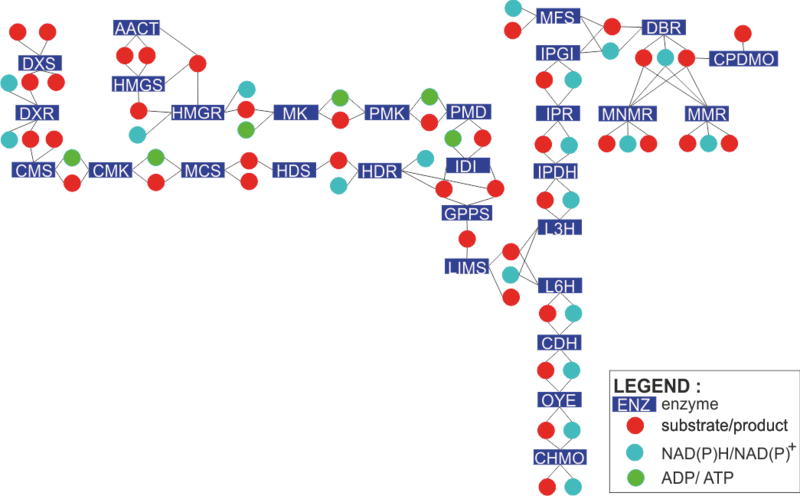
The engineered monoterpene network and its enzymatic reactions

To find out how each enzyme in the network is modelled, click on the rectangles in the figure on the left. Alternatively, you can click the enzyme names from the list below.

IPP and DMAPP Biosynthesis

Diphosphomelvalonate decarboxylase (DMD)

Hydroxymethylbutenyl diphosphate reductase (HMBPPR)

Limonene Biosynthesis

Geranyl diphosphate synthase (GPPS)

Limonene Synthase

Peppermint Biosynthesis

Limonene-3-hydroxylase (L3H)

Isopiperitenol Dehydrogenase (IPDH)

Isopiperitenol Reductase (IPR)

Isopulegone Isomerase (IPGI)

Mint Biosynthesis

Pulegone Reductase (PGR)

DBR

Menthone:Neomenthol reductase (MNMR)

Menthone:Menthol reductase (MMR)

Spearmint Biosynthesis

Limonene-6-Hydroxylase (L6H)

Carveol Dehydrogenase (CDH)

OYE

CHMO

Methanofuran Biosynthesis

Menthofuran synthase (MFS)

Rate laws used in the model

Reactions in these models are described reversibly using Michaelis-Menten rate law and Convenience kinetics

Convenience kinetics

Kinetic Parameters

Strategies for Estimating Kinetic Parameter Values

Using Equilibrium Constant (K_eq) in the reversible Michaelis-Menten equation

Using the equilibrium constant in the reversible Michaelis-Menten reaction reduces the need to obtain or estimate Vmax_reverse parameter value, which is often not available in literature.

Using the Haldane relationship, the equilibrium constant (K_eq) can be written as:

Failed to parse (Cannot store math image on filesystem.): {\color{Red}K_\mathrm{eq}} = \frac{Vmax_\mathrm{forward} * Km_\mathrm{product} }{Vmax_\mathrm{reverse} * Km_\mathrm{substrate}}

The reversible Michaelis-Menten rate equation can then be rewritten to contain the equilibrium constant (K_eq) instead of using the ratio of the V_max values.

Failed to parse (Cannot store math image on filesystem.): v_\mathrm{reaction} = Vmax_\mathrm{forward} * \cfrac {\cfrac{[S]}{Km_\mathrm{substrate}} * \left ( 1 - \cfrac {[P]}{[S]* \color{red}K_\mathrm{eq}} \right )} {1 + \cfrac {[S]}{Km_\mathrm{substrate}} + \cfrac {[P]}{Km_\mathrm{product}}}

where [S] and [P] corresponds to the concentration of the substrate and product respectively.

Calculating the Equilibrium Constant (K_eq)

The equilibrium constant can be calculated from the ratio of the forward and reverse reaction rates as described in the above section, given that the values for these rates are known. Unfortunately, the information for these values are often difficult to find, especially for reverse reaction rates (Vmax_reverse).

As an alternative, the equlibrium constant, K_eq, can also be calculated from the Gibbs free energy of a reaction, ΔG_r, using the Van't Hoff isotherm equation:

$-ΔG^° = -RT ln K$

and by dividing both sides of the equation with RT, and later take the exponents of both sides, the K_eq can be calculated by this equation:

$K_\mathrm{eq} = exp \left ( \cfrac {-ΔG^{°'}}{RT} \right )$

where;

Keq	Equilibrium constant
-ΔG°	Gibbs free energy change
R	Gas constant with a value of 8.31 JK-1mol-1
T	Temperature which is always expressed in kelvin

List of kinetic parameter values

Lists of values retrieved from published and unpublished sources for the kinetics of all the enzymes included in this study can be found here.

Abbreviations

List of abbreviations used in this study can be found here

Back to the main model page.