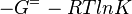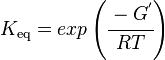Kinetic Model of Monoterpenoid Biosynthesis Wiki

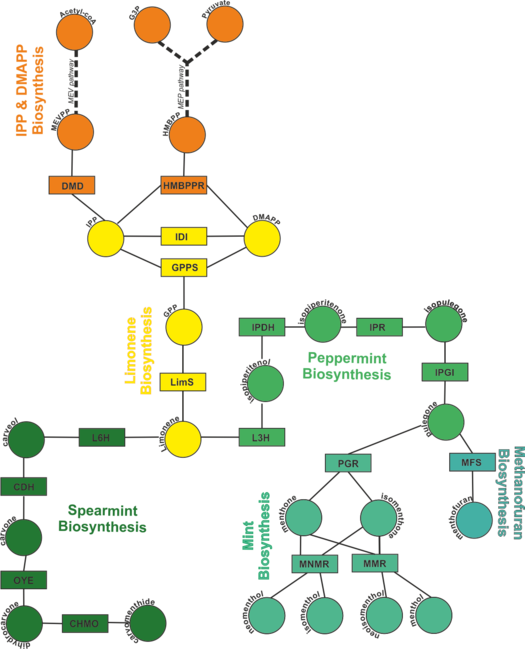
This wiki page describes the construction and simulation of a kinetic model of Monoterpenoid Biosynthesis.

Description of the model

To find out how each enzyme in the network is modelled, click on the rectangles in the figure on the left. Alternatively, you can click the enzyme names from the list below.

IPP and DMAPP Biosynthesis

Diphosphomelvalonate decarboxylase (DMD)

Hydroxymethylbutenyl diphosphate reductase (HMBPPR)

Limonene Biosynthesis

Geranyl diphosphate synthase (GPPS)

Limonene Synthase

Peppermint Biosynthesis

Limonene-3-hydroxylase (L3H)

Isopiperitenol Dehydrogenase (IPDH)

Isopiperitenol Reductase (IPR)

Isopulegone Isomerase (IPGI)

Mint Biosynthesis

Pulegone Reductase (PGR)

MNMR

MMR

Spearmint Biosynthesis

Limonene-6-Hydroxylase (L6H)

Carveol Dehydrogenase (CDH)

OYE

CHMO

Methanofuran Biosynthesis

Menthofuran synthase (MFS)

Reversible Michaelis-Menten equation

All reactions in this model are described using reversible Michaelis-Menten equation.

Kinetic Parameters

Strategies for Estimating Kinetic Parameter Values

Using Equilibrium Constant (K_eq) in the reversible Michaelis-Menten equation

Using the equilibrium constant in the reversible Michaelis-Menten reaction reduces the need to obtain or estimate Vmax_reverse parameter value, which is often not available in literature.

Using the Haldane relationship, the equilibrium constant (K_eq) can be written as:

Failed to parse (Cannot store math image on filesystem.): {\color{Red}K_\mathrm{eq}} = \frac{Vmax_\mathrm{forward} * Km_\mathrm{product} }{Vmax_\mathrm{reverse} * Km_\mathrm{substrate}}

The reversible Michaelis-Menten rate equation can then be rewritten to contain the equilibrium constant (K_eq) instead of using the ratio of the V_max values.

Failed to parse (Cannot store math image on filesystem.): v_\mathrm{reaction} = Vmax_\mathrm{forward} * \cfrac {\cfrac{[S]}{Km_\mathrm{substrate}} * \left ( 1 - \cfrac {[P]}{[S]* \color{red}K_\mathrm{eq}} \right )} {1 + \cfrac {[S]}{Km_\mathrm{substrate}} + \cfrac {[P]}{Km_\mathrm{product}}}

where [S] and [P] corresponds to the concentration of the substrate and product respectively.

Calculating the Equilibrium Constant (K_eq)

The equilibrium constant can be calculated from the ratio of the forward and reverse reaction rates as described in the above section, given that the values for these rates are known. Unfortunately, the information for these values are often difficult to find, especially for reverse reaction rates (Vmax_reverse).

As an alternative, the equlibrium constant, K_eq, can also be calculated from the Gibbs free energy of a reaction, ΔG_r, using the Van't Hoff isotherm equation:

$-ΔG^° = -RT ln K$

and by dividing both sides of the equation with RT, and later take the exponents of both sides, the K_eq can be calculated by this equation:

$K_\mathrm{eq} = exp \left ( \cfrac {-ΔG^{°'}}{RT} \right )$

where;

Keq	Equilibrium constant
-ΔG°	Gibbs free energy change
R	Gas constant with a value of 8.31 JK-1mol-1
T	Temperature which is always expressed in kelvin

List of kinetic parameter values

Lists of values retrieved from published and unpublished sources for the kinetics of all the enzymes included in this study can be found here.

Data gathering progress:

Enzyme	Pathway	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
01_GPPS	Limonene Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
01_L3H	Peppermint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2			VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
01_L6H	Spearmint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2			VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
01_MFS	Methanofuran Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
01_PGR	Mint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
02_CDH	Spearmint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
02_IPDH	Peppermint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
02_LimSynth	Limonene Biosynthesis				KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
02_MNMR (menthone)	Mint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
02a_IPDH	Spearmint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
03_IPR	Peppermint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
03_MMR (menthone)	Mint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
03_OYE	Spearmint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
04_CHMO	Spearmint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
04_IPGI	Peppermint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
04_MNMR (isomenthone)	Mint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
enzyme	Pathway	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]
04_MNMR (isomenthone)	Mint Biosynthesis	Keq	VmaxF	KmSub1	KmSub2	[Sub1]	[Sub2]	VmaxR	KmProd1	KmProd2	[Prod1]	[Prod2]

Abbreviations

List of abbreviations used in this study can be found here

Back to the main model page.