Difference between revisions of "Kinetic model of Central Metabolism"
(→Reactions) |
(→Description of the model) |
||
| Line 20: | Line 20: | ||
rect 261 920 284 943 [[Pyruvate kinase|PYK]] | rect 261 920 284 943 [[Pyruvate kinase|PYK]] | ||
rect 263 1007 283 1029 [[Lactate dehydrogenase|LDH]] | rect 263 1007 283 1029 [[Lactate dehydrogenase|LDH]] | ||
| − | rect 263 1119 285 1140 [[ | + | rect 263 1119 285 1140 [[Monocarboxylate (Lactate) transporter|MCT]] |
rect 532 953 554 978 [[Mitocondrial pyruvate metabolism|MPM]] | rect 532 953 554 978 [[Mitocondrial pyruvate metabolism|MPM]] | ||
rect 526 384 554 409 [[Adenylate kinase|AK]] | rect 526 384 554 409 [[Adenylate kinase|AK]] | ||
Revision as of 13:19, 26 March 2014
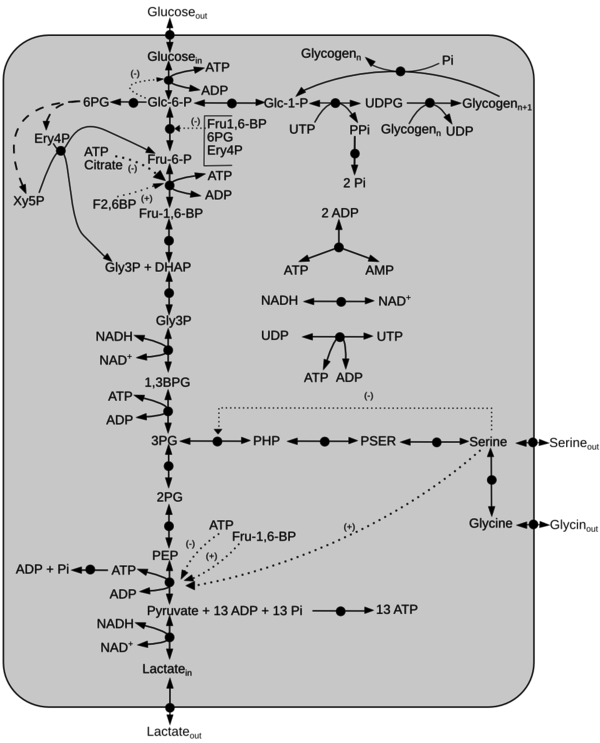
A kinetic model of glycolysis with serine activation is constructed from the literature data [1][2][3][4].
Description of the model
Schematic diagram of the model is gvien here. The dotted line represents activation(+) or inhibition(-) and the dashed arrow indicate Pentose Phosphate Pathway reactions not included in the model. Click on a reaction to have more information
Reactions
Details of the abbreviations for this model is listed here. Reactions of the model are listed below.
Initial concentration of the metabolites can be found here
Model File
The SBML file of the model can be found here.
Global parameters
The Vmax value in the paper "Modeling cancer glycolysis" is given in 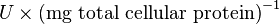 unit [1]. To homogenize the units it is then converted back to
unit [1]. To homogenize the units it is then converted back to 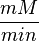 by multiplying
by multiplying 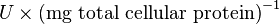 with 65 as the HeLa cell was incubated in
with 65 as the HeLa cell was incubated in 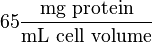 .
.
References
- ↑ 1.0 1.1 Marín-Hernández A, Gallardo-Pérez JC, Rodríguez-Enríquez S et al (2011). Modeling cancer glycolysis. Biochim Biophys Acta, 1807:755–767 (doi)
- ↑ Turnaev II, Ibragimova SS, Usuda Y et al (2006). Mathematical modeling of serine and glycine synthesis regulation in Escherichia coli. Proceedings of the fifth international conference on bioinformatics of genome regulation and structure 2:78–83
- ↑ Smallbone K, Stanford NJ (2013). Kinetic modeling of metabolic pathways: Application to serine biosynthesis. In: Systems Metabolic Engineering, Humana Press. pp. 113–121
- ↑ Palm, D.C. (2013). The regulatory design of glycogen metabolism in mammalian skeletal muscle (Ph.D.). University of Stellenbosch