Difference between revisions of "Transcription of a"
(→Parameters with uncertainty) |
(→Parameters with uncertainty) |
||
| Line 81: | Line 81: | ||
When deciding how to describe the uncertainty for this parameter we must take into consideration that the reported values are either calculated or derived with approximation from experiments and from other macromolecular properties. Additionally, some of the values correspond to mRNA transcription rates of different bacteria species (''E. coli''). This means that there might be a notable difference between actual parameter values and the ones reported in literature. These facts influence the quantification of the parameter uncertainty and therefore the shape of the corresponding distributions. Therefore, by assigning the appropriate weights to the parameter values and using the method described [[Quantification of parameter uncertainty#Design of probability distributions|'''here''']], the appropriate probability distributions were designed. | When deciding how to describe the uncertainty for this parameter we must take into consideration that the reported values are either calculated or derived with approximation from experiments and from other macromolecular properties. Additionally, some of the values correspond to mRNA transcription rates of different bacteria species (''E. coli''). This means that there might be a notable difference between actual parameter values and the ones reported in literature. These facts influence the quantification of the parameter uncertainty and therefore the shape of the corresponding distributions. Therefore, by assigning the appropriate weights to the parameter values and using the method described [[Quantification of parameter uncertainty#Design of probability distributions|'''here''']], the appropriate probability distributions were designed. | ||
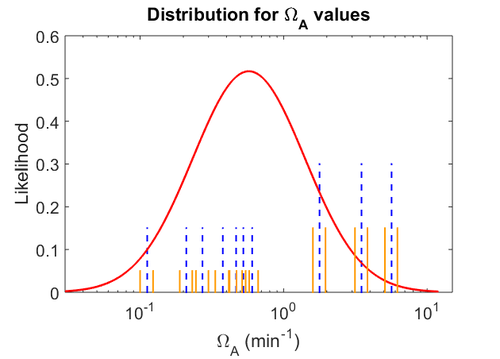
| − | Therefore, although the weight of the distribution is put on the | + | Therefore, although the weight of the distribution is put on the values calculated for ''S. coelicolor'' by setting <math> 0.57 min^{-1} </math> as the mode of the log-normal distribution for the <math>\Omega_{A}</math>, we wish to explore the full range of reported values. Thus, the confidence interval factor is set to <math>12.5</math> and the range where 95.45% of the values are found is between <math>0.0457</math> and <math>7.17</math> <math>min^{-1}</math>. |
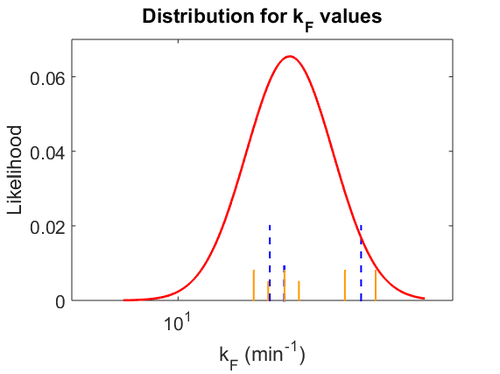
With regards to the firing rate <math>k_F</math>, the reported values are within the range of <math>18-33 min^{-1}</math> with the most probable values being <math>18-20 min^{-1}</math>. Since these values are reported as being the average rates (and <math>33 min^{-1}</math> being the maximum), we will also sample lower values, so the final sampling range will be around the values <math>10-33 min^{-1}</math>. The mode of the distribution is set to <math>20.4 min^{-1}</math> and the confidence interval factor is set to <math>1.74</math>. Therefore, the range where 95.45% of the values are found is between <math>12</math> and <math>35.6</math> <math>min^{-1}</math>. | With regards to the firing rate <math>k_F</math>, the reported values are within the range of <math>18-33 min^{-1}</math> with the most probable values being <math>18-20 min^{-1}</math>. Since these values are reported as being the average rates (and <math>33 min^{-1}</math> being the maximum), we will also sample lower values, so the final sampling range will be around the values <math>10-33 min^{-1}</math>. The mode of the distribution is set to <math>20.4 min^{-1}</math> and the confidence interval factor is set to <math>1.74</math>. Therefore, the range where 95.45% of the values are found is between <math>12</math> and <math>35.6</math> <math>min^{-1}</math>. | ||
| Line 87: | Line 87: | ||
The probability distributions for the parameters, adjusted accordingly in order to reflect the above values, are the following: | The probability distributions for the parameters, adjusted accordingly in order to reflect the above values, are the following: | ||
| − | [[Image: | + | [[Image:WA.png|500px]] |
[[Image:KFu.png|500px]] | [[Image:KFu.png|500px]] | ||
| Line 97: | Line 97: | ||
|- | |- | ||
|<math>\Omega_{A}</math> | |<math>\Omega_{A}</math> | ||
| − | |<math>0. | + | |<math>0.35405</math> |
| − | |<math>0. | + | |<math>0.95491</math> |
|- | |- | ||
|<math>k_{F}</math> | |<math>k_{F}</math> | ||
Revision as of 20:14, 25 January 2017
The scbA gene is transcribed into scbA mRNA (a).
Contents
Chemical equation
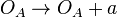 (maximum transcription in the scenario where the activating complex
(maximum transcription in the scenario where the activating complex 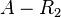 does not exist)
does not exist) 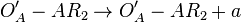 (maximum transcription in the scenario where the activating complex
(maximum transcription in the scenario where the activating complex 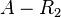 exists)
exists) 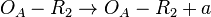 (basal transcription)
(basal transcription) Rate equation
![r= T_{A}\cdot [O_{A}]](/wiki/images/math/e/7/b/e7bcf235643659097dda4bfe871ef694.png)
![r= T_{A}\cdot [O_{A}'-AR_{2}]](/wiki/images/math/0/f/e/0feaaf54f19385cb881a2081f7ae35a3.png)
![r= T_{A_{basal}}\cdot [O_{A}-R_{2}]](/wiki/images/math/5/7/9/5796d8612a271421d5edf35506fc0dc5.png)
Parameters
The parameters of this reaction are the basal and maximum transcription rate of ScbA (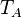 and
and 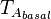 ).
These parameters are derived by the strength of the promoter (
).
These parameters are derived by the strength of the promoter (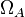 and
and 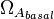 ) but also taking into account the transcriptional interference by the scbR promoter. In this model, we have assumed that the isolated promoter strength is equal to the number of transcripts produced per unit of time. Therefore, the parameters
) but also taking into account the transcriptional interference by the scbR promoter. In this model, we have assumed that the isolated promoter strength is equal to the number of transcripts produced per unit of time. Therefore, the parameters 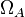 and
and 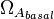 are assumed to be equal to the transcription rate constant of the isolated promoter. These parameter values were derived from published data on E.coli mRNA transcription rate and calculations based on genomic properties of Streptomyces coelicolor A3(2). Additionally, the firing rate (elongation initiation rate) constant (
are assumed to be equal to the transcription rate constant of the isolated promoter. These parameter values were derived from published data on E.coli mRNA transcription rate and calculations based on genomic properties of Streptomyces coelicolor A3(2). Additionally, the firing rate (elongation initiation rate) constant (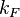 ) is needed. This parameter is also derived from literature and is sampled from the same distribution for both scbR and scbA promoters, but is then multiplied by a heterogeneity factor
) is needed. This parameter is also derived from literature and is sampled from the same distribution for both scbR and scbA promoters, but is then multiplied by a heterogeneity factor 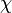 to calculate the final
to calculate the final 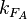 for the scbA promoter. The heterogeneity factor for each promoter is sampled from a xxx distribution.
for the scbA promoter. The heterogeneity factor for each promoter is sampled from a xxx distribution.
| Name | Value | Units | Value in previous GBL models [1] [2] | Remarks-Reference |
|---|---|---|---|---|
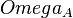
|
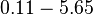 [3] [4] [5] [3] [4] [5]
|
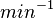
|
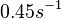 [1][2] [1][2]
(Range tested: (Bistability range: and |
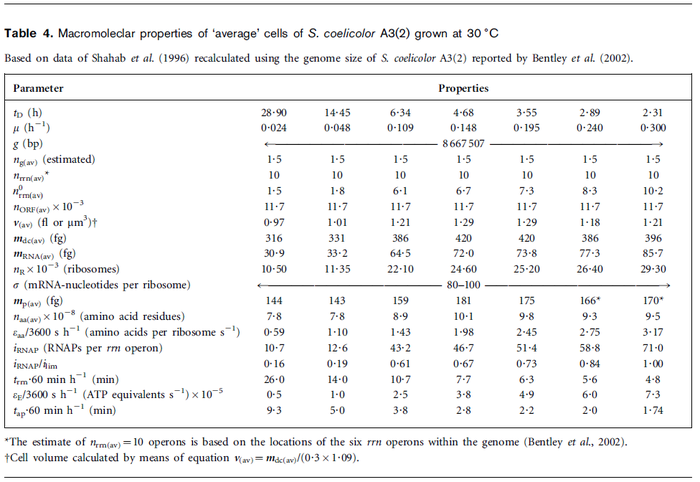
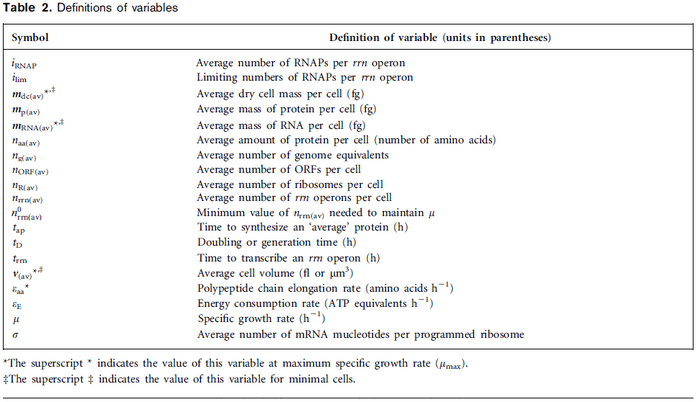
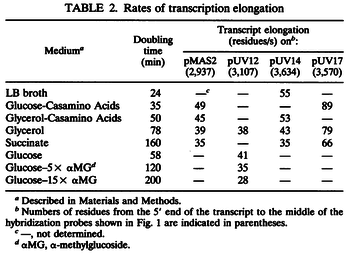
In a recent publication by R.A. Cox, genomic properties and macromolecular compositions of Streptomyces coelicolor A3(2) and E.coli were reported, along with equations that connect these properties. For S. coelicolor, the polypeptide elongation rate 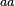 is reported to be 3.17 amino acids s-1, from which the mRNA elongation rate can be calculated according to Cox from the equation is reported to be 3.17 amino acids s-1, from which the mRNA elongation rate can be calculated according to Cox from the equation 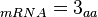 (factor 3 reflects the number of nucleotides per codon), therefore (factor 3 reflects the number of nucleotides per codon), therefore 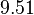 nucleotides nucleotides 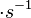 . As ScbA has 945 pb, the transcription rate constant can be calculated as per . As ScbA has 945 pb, the transcription rate constant can be calculated as per 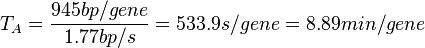 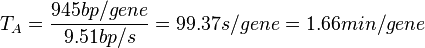 , thus resulting in final values of , thus resulting in final values of 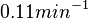 and and 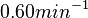 . .
Additionally, Bremer et al. have reported an mRNA transcription rate of 55 noucleotides/s for E. coli, a value which is also shared by R.A. Cox, while Vogel et al. have published a range of mRNA transcription rates in the range of 28-89 noucleotides/s, depending on different growth rates of E. coli. By the same calculations, the corresponding transcription rate constants are |
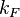
|
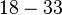 [6] [7] [8] [6] [7] [8]
|
|
N/A | Pai et al. reported a typical transcription initiation rate in QS systems to be 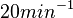 . .
 Pai et al. 2009 [6] This value is also supported by Kennell et al. who calculated the transcription initiation rates from experimental data derived from in vitro experiments using E. coli. The results showed one initiation every 3.3 sec (therefore transcription rate 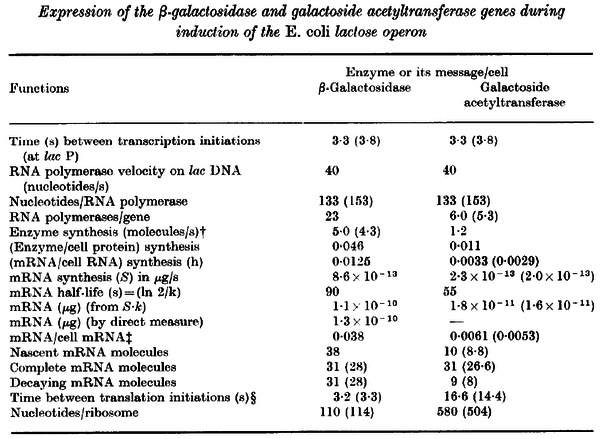 Kennell et al. 1977 [8] Finally, Tadmor et al. reported a maximum transcription initiation rate of 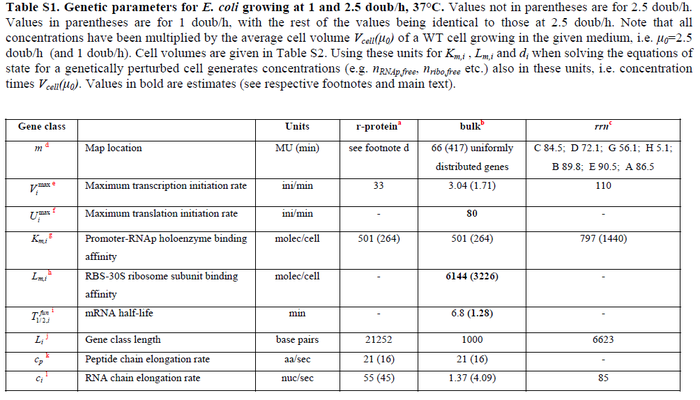 Tadmor et al. 2008 [7] |
From the 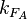 and the
and the 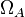 and
and 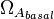 the basal and maximal occupancy (
the basal and maximal occupancy (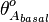 and
and 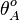 ) of the isolated scbA promoter can be calculated as per
) of the isolated scbA promoter can be calculated as per 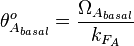 and
and 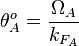 .
Also, by employing the ratio of the bound vs. total promoter
.
Also, by employing the ratio of the bound vs. total promoter ![\rho_{A}=\frac{[O_{A}-R_{2}]}{[O_{A}]+[O_{A}-R_{2}]}](/wiki/images/math/b/8/8/b8879ff36035d4547820f382edcc7be1.png) , the effective occupancy of the isolated scbA promoter can be calculated as per
, the effective occupancy of the isolated scbA promoter can be calculated as per 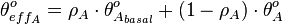 . Similarly, the effective occupancy of the isolated scbR promoter (
. Similarly, the effective occupancy of the isolated scbR promoter (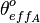 )is calculated as described in theTranscription of r.
Therefore, the promoter relative activity is equal to
)is calculated as described in theTranscription of r.
Therefore, the promoter relative activity is equal to 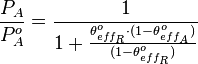 and the final basal and maximal transcription rate constants are calculated as per
and the final basal and maximal transcription rate constants are calculated as per 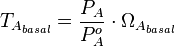 and
and 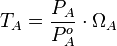 respectively.
respectively.
Parameters with uncertainty
When deciding how to describe the uncertainty for this parameter we must take into consideration that the reported values are either calculated or derived with approximation from experiments and from other macromolecular properties. Additionally, some of the values correspond to mRNA transcription rates of different bacteria species (E. coli). This means that there might be a notable difference between actual parameter values and the ones reported in literature. These facts influence the quantification of the parameter uncertainty and therefore the shape of the corresponding distributions. Therefore, by assigning the appropriate weights to the parameter values and using the method described here, the appropriate probability distributions were designed.
Therefore, although the weight of the distribution is put on the values calculated for S. coelicolor by setting 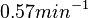 as the mode of the log-normal distribution for the
as the mode of the log-normal distribution for the 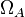 , we wish to explore the full range of reported values. Thus, the confidence interval factor is set to
, we wish to explore the full range of reported values. Thus, the confidence interval factor is set to 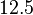 and the range where 95.45% of the values are found is between
and the range where 95.45% of the values are found is between 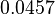 and
and 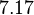
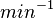 .
.
With regards to the firing rate 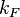 , the reported values are within the range of
, the reported values are within the range of 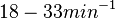 with the most probable values being
with the most probable values being 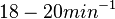 . Since these values are reported as being the average rates (and
. Since these values are reported as being the average rates (and 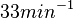 being the maximum), we will also sample lower values, so the final sampling range will be around the values
being the maximum), we will also sample lower values, so the final sampling range will be around the values 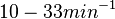 . The mode of the distribution is set to
. The mode of the distribution is set to 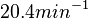 and the confidence interval factor is set to
and the confidence interval factor is set to 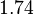 . Therefore, the range where 95.45% of the values are found is between
. Therefore, the range where 95.45% of the values are found is between 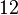 and
and 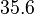
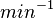 .
.
The probability distributions for the parameters, adjusted accordingly in order to reflect the above values, are the following:
The location and scale parameters of the distribution are:
| Parameter | μ | σ |
|---|---|---|
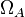
|
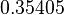
|
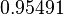
|
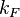
|
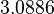
|
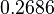
|
References
- ↑ 1.0 1.1 1.2 S. Mehra, S. Charaniya, E. Takano, and W.-S. Hu. A bistable gene switch for antibiotic biosynthesis: The butyrolactone regulon in streptomyces coelicolor. PLoS ONE, 3(7), 2008.
- ↑ 2.0 2.1 2.2 A. Chatterjee, L. Drews, S. Mehra, E. Takano, Y.N. Kaznessis, and W.-S. Hu. Convergent transcription in the butyrolactone regulon in streptomyces coelicolor confers a bistable genetic switch for antibiotic biosynthesis. PLoS ONE, 6(7), 2011.
- ↑ 3.0 3.1 3.2 Cox RA. Quantitative relationships for specific growth rates and macromolecular compositions of Mycobacterium tuberculosis, Streptomyces coelicolor A3(2) and Escherichia coli B/r: an integrative theoretical approach. Microbiology. 2004 May;150(Pt 5):1413-26.
- ↑ 4.0 4.1 Bremer H., Yuan D. RNA chain growth-rate in Escherichia coli, Journal of Molecular Biology, 1968; 38:(2), p. 163-180
- ↑ 5.0 5.1 Vogel U., Jensen KF. The RNA chain elongation rate in Escherichia coli depends on the growth rate. Journal of Bacteriology. 1994;176(10):2807-2813.
- ↑ 6.0 6.1 Pai, A. and You, L. Optimal tuning of bacterial sensing potential. Mol Syst Biol. 2009; 5: 286
- ↑ 7.0 7.1 Tadmor AD, Tlusty T. A Coarse-Grained Biophysical Model of E. coli and Its Application to Perturbation of the rRNA Operon Copy Number. PLoS Comput Biol (2008); 4(5): e1000038. doi: 10.1371/journal.pcbi.1000038
- ↑ 8.0 8.1 Kennell D., Riezman H. Transcription and translation initiation frequencies of the Escherichia coli lac operon. J. Mol. Biol. 1977; 114(1):1-21


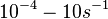 )
)
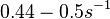
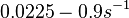
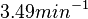 and
and 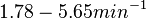 .
.
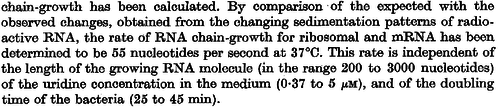
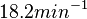 ).
).