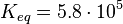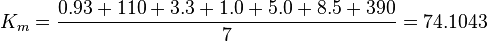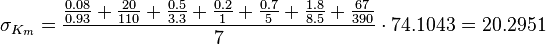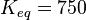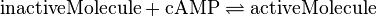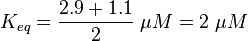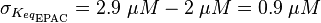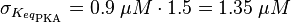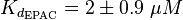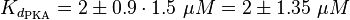Difference between revisions of "Equilibrium constants"
m |
m |
||
| Line 1: | Line 1: | ||
{{:Template:MAPK_Template}} | {{:Template:MAPK_Template}} | ||
| − | <h2> Ras/Rap1-Activation | + | <h2> Ras/Rap1-Activation</h2> |
The only phosphorylation for which an individual equilibrium constant is calculated according to the different measured equilibrium binding constants is the activation of Ras by Sos. Because of the fact that the equilibrium constant is not influenced by the enzyme the same equilibrium constant for the activation and inactivation process an be used. | The only phosphorylation for which an individual equilibrium constant is calculated according to the different measured equilibrium binding constants is the activation of Ras by Sos. Because of the fact that the equilibrium constant is not influenced by the enzyme the same equilibrium constant for the activation and inactivation process an be used. | ||
| Line 13: | Line 13: | ||
<math> 3.07 \cdot 3.95480 \cdot 10^{-2} = 0.48110 </math> | <math> 3.07 \cdot 3.95480 \cdot 10^{-2} = 0.48110 </math> | ||
| + | |||
| + | <h2> Ras/Rap1-Inactivation</h2> | ||
| + | The inactivation step is a hydrolysis of GTP catalysed by Gap. The equilibrium constant of ATP hydrolysis and as an uncertainty the [[Calculation of the averaged relative error|averaged relative error of the measured errors]] is used. | ||
| + | |||
| + | <math>K_{eq} = 5.8 \cdot 10^{5}</math><ref name="Manchester1980">Manchester K.L. Free Energy, ATP Hydrolysis and Phosphorylation Potential. Biochemical Education 8(3) pp.70-72 ([http://onlinelibrary.wiley.com/doi/10.1016/0307-4412%2880%2990043-6/pdf Wiley Online Library])</ref> | ||
| + | |||
<h2> C3G-Activation </h2> | <h2> C3G-Activation </h2> | ||
| Line 44: | Line 50: | ||
The equilibrium constant of the dephosphorylation of glucose-6-phosphate is used (glucose 6-P<sup>-</sup> + H<sub>2</sub>O ⇌ glucose + H<sub>2</sub>PO<sub>4</sub><sup>-</sup>).As an uncertainty is the [[Calculation of the averaged relative error|averaged relative error of the measured errors used]]. | The equilibrium constant of the dephosphorylation of glucose-6-phosphate is used (glucose 6-P<sup>-</sup> + H<sub>2</sub>O ⇌ glucose + H<sub>2</sub>PO<sub>4</sub><sup>-</sup>).As an uncertainty is the [[Calculation of the averaged relative error|averaged relative error of the measured errors used]]. | ||
| − | <math>K_{eq} = 750 </math><ref name="Manchester1980"> | + | <math>K_{eq} = 750 </math><ref name="Manchester1980"></ref> |
Latest revision as of 11:22, 12 June 2014
Ras/Rap1-Activation
The only phosphorylation for which an individual equilibrium constant is calculated according to the different measured equilibrium binding constants is the activation of Ras by Sos. Because of the fact that the equilibrium constant is not influenced by the enzyme the same equilibrium constant for the activation and inactivation process an be used.
Further assuming that the process of GDP-GTP exchange at the Rap enzyme is similar to that at Ras the calculated equilibrium constant is used for these reaction, too.
Keq = 3.07
For more information about how this is calculated please see here.
As an uncertainty is the averaged relative error of the measured errors used.
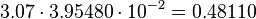
Ras/Rap1-Inactivation
The inactivation step is a hydrolysis of GTP catalysed by Gap. The equilibrium constant of ATP hydrolysis and as an uncertainty the averaged relative error of the measured errors is used.
C3G-Activation
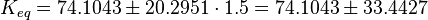
| Notes | References |
|---|---|
| The equilibrium constant is calculated by taking the average of various measured dissociation constants of different peptides to a SH2 domain. For the standard deviation the relative standard deviation of the single measurements is calculated and the same relative error for the calculated averaged equilibrium constant is assumed. The result is then increased by 1.5. Calculation
|
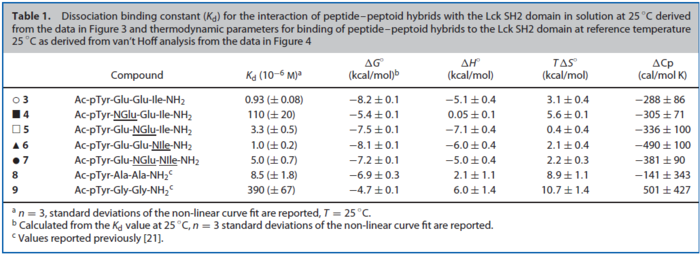 Dekker et al. (2010)[2] |
Phosphorylation Steps
The equilibrium constant for phosphorylation varies according to the conditions. Under the conditions of pH7, free [Mg2+] = 1,0 mmol/l, I = 0.25 mol/l, T = 38 °C the equilibrium constant by the creatine kinase is 177 ± 7 (n=8) (Teague et al. 1992)[3] . The error is increased by 1.5 and the constant is used for all phosphorylation/dephosphorylation steps.
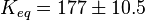
Dephosphorylation
The equilibrium constant of the dephosphorylation of glucose-6-phosphate is used (glucose 6-P- + H2O ⇌ glucose + H2PO4-).As an uncertainty is the averaged relative error of the measured errors used.
EPAC/PKA-Activation and Inactivation
Activation by Cilostamide:
Xu et al. (2010) [4] modelled the activation due to Cilostamide as irreversible, so it can be assumed that the equilibrium is far on the product side and therefore the equilibrium constant is high. We used Keq = 109.
Activation by Agonist and Inactivation:
|
For our model we assumed that the equilibrium constant is in the range of cAMP binding to either non-mutated EPAC1 or to mutated EPAC1. To gain the final parameter both values are averaged. The cAMP analogon used by Xu et al. (2010)[4] is not listed. However it can be seen that equilibrium constants for different analoga differ widely and therefore it is assumed that only 68% of the values are in the range of both values. This means the difference between one value and the calculated mean is set to σ. However, we used this only as working hypothesis, because firstly this reaction was modelled as Michaelis-Menten reaction, which does not mirror the mechanism, secondly the cAMP level is not included in our model and thirdly the equilibriums constant should be dimensionless. This reaction should late be changed to a binding process, in which no equilibirum constant is needed. Reaction measured
Calculation:
The equilibrium constant for the activation of PKA is assumed to be similar to the one of EPAC, because of the similaritiy of the activation process, however the uncertainty is increased by the factor of 1.5.
Result:
|
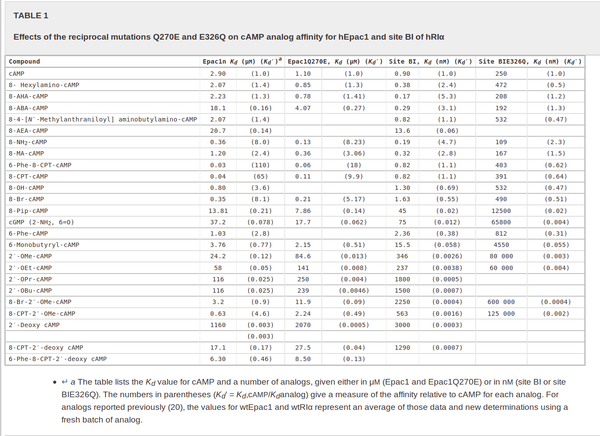 Dao et al. (2006)[5] |
References
- ↑ 1.0 1.1 Manchester K.L. Free Energy, ATP Hydrolysis and Phosphorylation Potential. Biochemical Education 8(3) pp.70-72 (Wiley Online Library)
- ↑ Dekker F.J., Mol N.J.D.E., and Liskamp R.M.J.(2010)"Thermodynamics of phosphotyrosine peptide-peptoid hybrids binding to the p56lck SH2 domain."J Pept Sci 16.7:322-328. DOI: 10.1002/psc.1242. (pmid:20552566)
- ↑ Teague WE Jr and Dobson G.P. (1992) "Effect of temperature on the creatine kinase equilibrium." J Biol Chem 267.20:14084-14093 (pmid:1629208)
- ↑ 4.0 4.1 Tian-Rui Xu et al. (2010) "Inferring signaling pathway topologies from multiple perturbation measurements of specific biochemical species." Sci Signal. 3(134):ra20. (pmid:20234003)
- ↑ Dao K.K. et al. (2006) "Epac1 and cAMP-dependent protein kinase holoenzyme have similar cAMP affinity, but their cAMP domains have distinct structural features and cyclic nucleotide recognition." J Biol Chem 281.30:21500-21511 (pmid:16728394)