Quantification of parameter uncertainty
In order to create the probability distributions, the location and scale parameters 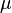 and
and 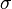 were required. These can be easily calculated from the mean and standard deviation of the available sample data. However in many cases, there were very little or no reported values for a parameter, or there was a minimum and maximum reported value. It was therefore necessary to come up with an alternative way to derive them which at the same time would be understandable to experimentalists, without demanding complicated mathematical terms and calculations.
were required. These can be easily calculated from the mean and standard deviation of the available sample data. However in many cases, there were very little or no reported values for a parameter, or there was a minimum and maximum reported value. It was therefore necessary to come up with an alternative way to derive them which at the same time would be understandable to experimentalists, without demanding complicated mathematical terms and calculations.
In order to achieve this, the mode of the log-normal distribution (global maximum) and its symmetric properties were employed. Log-normal distributions are symmetrical in the sense that values that are 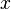 times larger than the most likely estimate, are just as plausible as values that are
times larger than the most likely estimate, are just as plausible as values that are 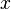 times smaller. More specifically, the mode of the distribution is the value
times smaller. More specifically, the mode of the distribution is the value 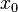 for which the condition
for which the condition 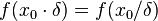 for all real numbers
for all real numbers 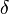 , (where
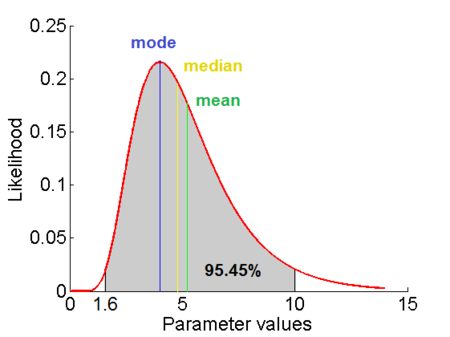
, (where 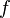 is the probability density function) is fulfilled. Hence, the user has to decide on a most plausible value for each parameter, which is set as the mode (global maximum) of the corresponding distribution (Probability Density Function or PDF), and on a range within which lie 95.45% of the values. The latter is linked to the mode via a multiplicative factor, which we call "Confidence Interval Factor". If the mode is multiplied or divided by the CI factor, the range within which 95.45% of the values are found is calculated. For instance, if the most plausible value for a parameter is
is the probability density function) is fulfilled. Hence, the user has to decide on a most plausible value for each parameter, which is set as the mode (global maximum) of the corresponding distribution (Probability Density Function or PDF), and on a range within which lie 95.45% of the values. The latter is linked to the mode via a multiplicative factor, which we call "Confidence Interval Factor". If the mode is multiplied or divided by the CI factor, the range within which 95.45% of the values are found is calculated. For instance, if the most plausible value for a parameter is 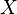 and the confidence interval multiplicative factor is
and the confidence interval multiplicative factor is 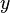 , then the mode of the distribution is set as
, then the mode of the distribution is set as 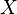 the range where 95.45% of the plausible values are found is
the range where 95.45% of the plausible values are found is ![[\frac{X}{y},X\cdot y]](/wiki/images/math/e/d/2/ed2bf0bf688aea7be4016cbe08252a9d.png) .
.
Based on these values, a two-by-two system of the equations containing the cumulative distribution function (CDF) and the mode is solved, in order to derive the location parameter 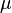 and the scale parameter
and the scale parameter 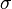 of the corresponding log-normal distribution. The equations are the following:
of the corresponding log-normal distribution. The equations are the following:
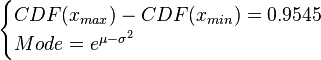
where ![CDF= \frac{1}{2}+\frac{1}{2} \mathrm{erf} \Big[\frac{lnx-\mu}{\sqrt{2}\sigma}\Big]](/wiki/images/math/e/8/a/e8ae5ac9150ce995145e521cb6f11e4e.png) and
and 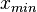 and
and 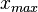 are the lower and upper bounds of the confidence interval. By substituting these into the previous equation the final form of the system is obtained:
are the lower and upper bounds of the confidence interval. By substituting these into the previous equation the final form of the system is obtained:
![\begin{cases}\frac{1}{2} \mathrm{erf} \Big[\frac{lnx_{max}-\mu}{\sqrt{2}\sigma}\Big]-\frac{1}{2} \mathrm{erf} \Big[\frac{lnx_{min}-\mu}{\sqrt{2}\sigma}\Big]=0.9545\\
Mode=e^{\mu-\sigma^{2}}\end{cases}](/wiki/images/math/9/1/1/91131156cbe90c34a6648eacf5d63c46.png)
In this way, the 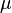 and
and 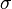 parameters are obtained and from them it is easy to calculate any property in the distribution (i.e. geometric mean, variance etc.)
parameters are obtained and from them it is easy to calculate any property in the distribution (i.e. geometric mean, variance etc.)
Additionally, for the parameters that are interconnected (i.e. forward and backward reaction rates) a bivariate distribution was created between 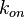 ,
, 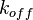 and
and 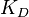 , in order to account for thermodynamic consistency. As the multivariate system requires a linear dependency between the two marginal distributions, two of the parameters will be independent and the third will be dependent on them. For instance, if the two marginal distributions are
, in order to account for thermodynamic consistency. As the multivariate system requires a linear dependency between the two marginal distributions, two of the parameters will be independent and the third will be dependent on them. For instance, if the two marginal distributions are 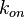 and
and 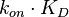 (=
(=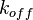 ),
), 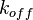 is dependent on the values of
is dependent on the values of 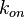 and
and 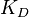 . The parameter with the largest geometric coefficient of variation (
. The parameter with the largest geometric coefficient of variation (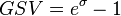 ) is usually set as the dependent one. Any product of two log-normal random variables is also log-normally distributed. Therefore, for the two log-normal distributions
) is usually set as the dependent one. Any product of two log-normal random variables is also log-normally distributed. Therefore, for the two log-normal distributions 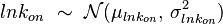 and
and 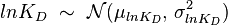 , their product
, their product 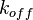 will be the log-normal distribution
will be the log-normal distribution 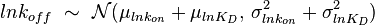 and its parameters will be
and its parameters will be 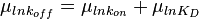 ,
, 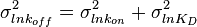 .
.
A similar strategy applies for the quotient of two log-normal distributions, although in this case the parameter 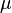 will be derived by the formula
will be derived by the formula 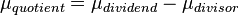 . The formula for the calculation of the parameter
. The formula for the calculation of the parameter 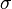 does not change.
does not change.
Thus, it becomes easy to transform the two marginal distributions 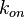 and
and 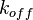 to normal ones, through the natural logarithm. The problem can therefore be reduced to the case of a multivariate normal distribution generated by the formula
to normal ones, through the natural logarithm. The problem can therefore be reduced to the case of a multivariate normal distribution generated by the formula
Failed to parse (syntax error): f(x,y)= \frac{1}{2 \pi \sigma_X \sigma_Y \sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}\left[ \frac{(x-\mu_X)^2}{\sigma_X^2} + \frac{(y-\mu_Y)^2}{\sigma_Y^2} - \frac{2\rho(x-\mu_X)(y-\mu_Y)}{\sigma_X \sigma_Y}\right] \right)\\
where 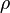 is the correlation between
is the correlation between 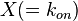 and
and 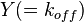 and
and 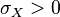 and
and 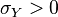 . In this case,
. In this case, 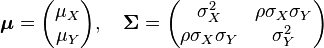 (covariance matrix).
(covariance matrix).
The required parameter values are obtained by generating samples from the multivariate normal distribution and then exponentiating the results. In order to avoid errors that are introduced to the correlation matrix during the exponentiation, a matlab function called Multivariate Lognormal Simulation with Correlation (MVLOGNRAND) is used, which makes up for these errors.