Difference between revisions of "Binding of R2 to C"
(→Parameters with uncertainty) |
(→Parameters with uncertainty) |
||
| Line 79: | Line 79: | ||
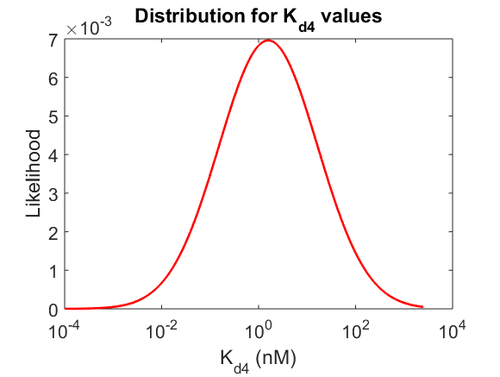
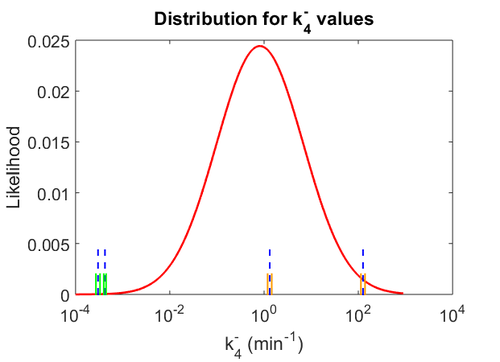
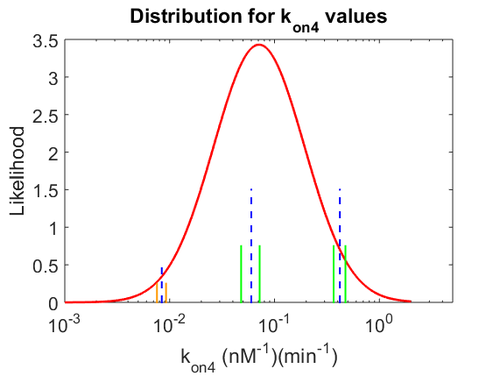
The probability distributions for the three parameters, adjusted accordingly in order to reflect the above values, are the following: | The probability distributions for the three parameters, adjusted accordingly in order to reflect the above values, are the following: | ||
| − | [[Image: | + | [[Image:KD4u.png|500px]] [[Image:K4u.png|500px]] [[Image:Kon4u.png|500px]] |
The correlation matrix which is necessary to define the relationship between the two marginal distributions (<math>K_{d4}</math>,<math>k^{-}_{4}</math>) of the bivariate system is derived by employing random values generated by the two distributions. | The correlation matrix which is necessary to define the relationship between the two marginal distributions (<math>K_{d4}</math>,<math>k^{-}_{4}</math>) of the bivariate system is derived by employing random values generated by the two distributions. | ||
Revision as of 18:33, 18 January 2017
SCBs (C) bind to ScbR homo-dimer (R2) and inactivate its repressing activity.
Contents
Chemical equation
The exact mechanism is still unclear, however in our model we assumed that two SCBs bind to the ScbR homo-dimer.
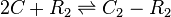
Rate equation
![r= \frac{k^{-}_{4}}{K_{d4}}\cdot [C]^{2}\cdot [R_{2}] - k^{-}_{4}\cdot [C_{2}-R_{2}]](/wiki/images/math/4/2/8/428673ce5611c43117d8088e36fbbdc1.png)
Parameters
The parameters of this reaction are the dissociation constant for binding of SCB to ScbR (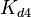 ) and the dissociation rate for binding of SCB to ScbR (
) and the dissociation rate for binding of SCB to ScbR (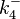 ). ScbR is a member of the TetR family of repressors, named after the member of this group which is the most completely characterized, the TetR repressor protein. TetR binds to the operator tetO, repressing its own expression and that of the efflux determinant tetA. However, [MgTc]+ binds to TetR and thus the affinity of the later for the operator tetO is 9-fold reduced. This procedure is similar to ScbR binding to OR and OA and repressing its own expression and the expression of ScbA, while binding to SCBs reduces its affinity for the two operators. Therefore parameter values were derived from published data on the TetR-[MgTc]+ and TetR-Tc (without Mg+) interactions.
). ScbR is a member of the TetR family of repressors, named after the member of this group which is the most completely characterized, the TetR repressor protein. TetR binds to the operator tetO, repressing its own expression and that of the efflux determinant tetA. However, [MgTc]+ binds to TetR and thus the affinity of the later for the operator tetO is 9-fold reduced. This procedure is similar to ScbR binding to OR and OA and repressing its own expression and the expression of ScbA, while binding to SCBs reduces its affinity for the two operators. Therefore parameter values were derived from published data on the TetR-[MgTc]+ and TetR-Tc (without Mg+) interactions.
| Name | Value | Units | Value in previous GBL models [1] [2] | Remarks-Reference |
|---|---|---|---|---|
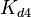
|
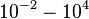 [3] [4] [5] [6] [7] [3] [4] [5] [6] [7]
|
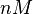
|
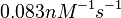
(Range tested: (Bistability range: and |
According to Hillen et al. and Orth et al. the association constant for TetR-Tc binding is in the ~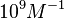 range in presence of Mg2+, as determined by in vitro measurements, therefore a Kd= ~ range in presence of Mg2+, as determined by in vitro measurements, therefore a Kd= ~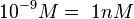
On the other hand, Kedracka-Krok et al. conducted stopped-flow measurements using TetR overproduced in Escherichia coli strain RB 791. They consequently reported an association constant Ka= Finally, Schubert et al. reported Mg2+ independent KAs of  Schubert et al. 2004[7] |
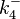
|
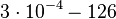 [3] [7] [3] [7]
|
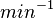
|
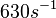
(Range tested: (Bistability range: and |
According to Kedracka-Krok et al. the unbinding rate for the TetR-Tc complex is 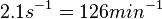 in absence of Mg2+ and in absence of Mg2+ and 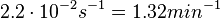 in presence of Mg2+ (see figure above). in presence of Mg2+ (see figure above).
However, Schubert et al. reported dissociation rates of In order to quantify the dependency between the parameters, a distribution for |
Parameters with uncertainty
When deciding how to describe the uncertainty for each parameter there are a few points to be taken into consideration. Firstly, the values reported in literature are spread in a relatively large range and correspond to TetR and TetR mutant proteins. Additionally, most of the values were acquired by in vitro testing. This means that there might be a notable difference between actual parameter values and the ones reported in literature. These facts influence the quantification of the parameter uncertainty and therefore the shape of the corresponding distributions. Therefore, by assigning the appropriate weights to the parameter values and using the method described here, the appropriate probability distributions were designed.
With regards to the 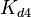 the value that is mostly reported in different publications is
the value that is mostly reported in different publications is 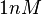 , therefore we put the weight of the distribution in the range
, therefore we put the weight of the distribution in the range 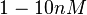 and we consider as least likely the larger values. Therefore, the mode of the log-normal distribution is
and we consider as least likely the larger values. Therefore, the mode of the log-normal distribution is 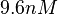 and the confidence interval factor is
and the confidence interval factor is 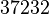 . Thus the range where 95.45% of the values are found is between
. Thus the range where 95.45% of the values are found is between 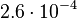 and
and 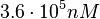 . (Note: This distribution represents our initial beliefs about the system but is redefined as explained below, in order to account for the thermodynamic consistency of the system.)
. (Note: This distribution represents our initial beliefs about the system but is redefined as explained below, in order to account for the thermodynamic consistency of the system.)
The smaller values reported by Schubert et al. (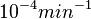 ) are also considered least likely for
) are also considered least likely for 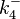 . The mode of the log-normal distribution for
. The mode of the log-normal distribution for 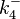 is calculated as
is calculated as 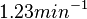 and the confidence interval factor is
and the confidence interval factor is 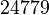 . In this way the range where 95.45% of the values are found is between
. In this way the range where 95.45% of the values are found is between 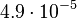 and
and 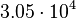
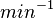 .
.
Finally, the probability distribution for 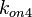 is defined accordingly, in order to allow the exploration of the full range of the values retrieved from literature. Therefore, the mode is set to
is defined accordingly, in order to allow the exploration of the full range of the values retrieved from literature. Therefore, the mode is set to 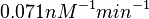 and the confidence interval factor is
and the confidence interval factor is 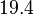 . In this way the range where 95.45% of the values are found is between 0.0037 and 1.3802
. In this way the range where 95.45% of the values are found is between 0.0037 and 1.3802 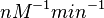 .
.
Since the three parameters are interdependent, thermodynamic consistency also needs to be taken into account. This is achieved by creating a bivariate system as described here. Since 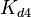 is the parameter with the largest geometric coefficient of variation, this is set as the dependent parameter as per:
is the parameter with the largest geometric coefficient of variation, this is set as the dependent parameter as per: 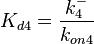 , and an updated probability distribution is defined. The location and scale parameters of
, and an updated probability distribution is defined. The location and scale parameters of 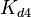 (μ=7.684 and σ=2.6711) were calculated from those of
(μ=7.684 and σ=2.6711) were calculated from those of 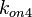 and
and 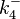 .
The probability distributions for the three parameters, adjusted accordingly in order to reflect the above values, are the following:
.
The probability distributions for the three parameters, adjusted accordingly in order to reflect the above values, are the following:
The correlation matrix which is necessary to define the relationship between the two marginal distributions (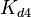 ,
,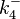 ) of the bivariate system is derived by employing random values generated by the two distributions.
) of the bivariate system is derived by employing random values generated by the two distributions.
The final parameters of the distributions of the multivariate system are:
| Parameter | μ | σ | Correlation matrix |
|---|---|---|---|
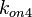
|
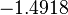
|
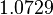
|
N/A |
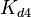
|
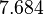
|
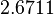
|
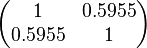
|
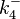
|
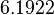
|
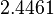
|
The multivariate system of the normal distributions (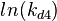 and
and 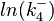 ) and the resulting samples of values are presented in the following figure:
) and the resulting samples of values are presented in the following figure:
In this way, a system of distributions is created where each distribution is described and constrained by the other two. Therefore, the parameters will be sampled by the two marginal distributions in a way consistent with our beliefs and with the relevant thermodynamic constraints.
References
- ↑ 1.0 1.1 1.2 S. Mehra, S. Charaniya, E. Takano, and W.-S. Hu. A bistable gene switch for antibiotic biosynthesis: The butyrolactone regulon in streptomyces coelicolor. PLoS ONE, 3(7), 2008.
- ↑ 2.0 2.1 2.2 A. Chatterjee, L. Drews, S. Mehra, E. Takano, Y.N. Kaznessis, and W.-S. Hu. Convergent transcription in the butyrolactone regulon in streptomyces coelicolor confers a bistable genetic switch for antibiotic biosynthesis. PLoS ONE, 6(7), 2011.
- ↑ 3.0 3.1 3.2 3.3 Sylwia Kedracka-Krok, Andrzej Gorecki, Piotr Bonarek, and Zygmunt Wasylewski. Kinetic and Thermodynamic Studies of Tet Repressor−Tetracycline Interaction. Biochemistry 2005 44 (3), 1037-1046
- ↑ Kamionka A, Bogdanska-Urbaniak J, Scholz O, Hillen W. Two mutations in the tetracycline repressor change the inducer anhydrotetracycline to a corepressor. Nucleic Acids Research. 2004;32(2):842-847.
- ↑ 5.0 5.1 Orth P., Schnappinger D, Hillen W, Saenger W, Hinrichs W. Structural basis of gene regulation by the tetracycline inducible Tet repressor-operator system. Nature Structural & Molecular Biology, 2000;7(3):215-9.
- ↑ 6.0 6.1 Hillen W., Berens C. Mechanisms underlying expression of Tn10 encoded tetracycline resistance. Annu Rev Microbiol. 1994;48:345-69.
- ↑ 7.0 7.1 7.2 Schubert P., Pfleiderer K., Hillen W. Tet repressor residues indirectly recognizing anhydrotetracycline. Eur J Biochem. 2004 Jun;271(11):2144-52.


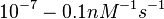 )
)
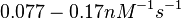
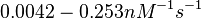


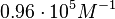 in absence of Mg2+ (therefore a Kd=
in absence of Mg2+ (therefore a Kd=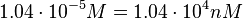 ) and an association constant Ka=
) and an association constant Ka=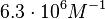 for binding of TetR to [Tc-Mg]+ (therefore a Kd=
for binding of TetR to [Tc-Mg]+ (therefore a Kd=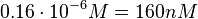 ).
).
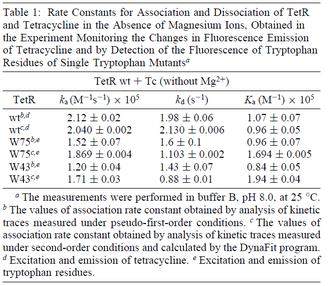

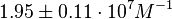 and
and 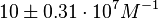
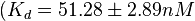 and
and 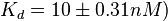 and Mg2+ dependent KAs of
and Mg2+ dependent KAs of 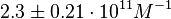 and
and 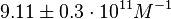
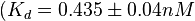 and
and 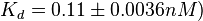 . The data was derived from in vitro and in vivo measurements in E. coli K12, strains DH5a and WH207.
. The data was derived from in vitro and in vivo measurements in E. coli K12, strains DH5a and WH207.
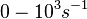 )
)
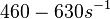
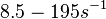
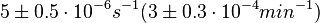 and
and 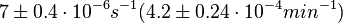 (see table above).
(see table above).
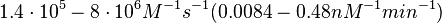 . These values will be used to define the corresponding probability distribution.
. These values will be used to define the corresponding probability distribution.