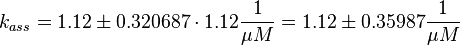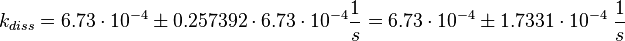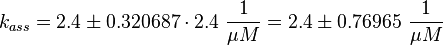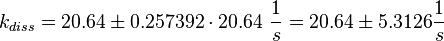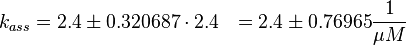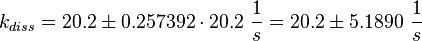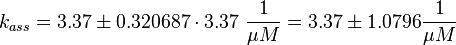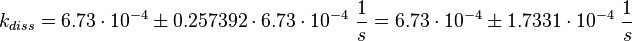Ras-Activation
Binding Reaction
Michaelis-Menten
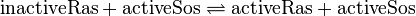
Mass Action
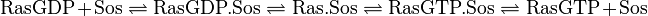
Kinetic equation
Michaelis-Menten
![v_{\text{Ras-Activation}} = \frac{k_{cat} \cdot [\text{activeSos}] \cdot [\text{inactiveRas}] \cdot (1-\frac{[\text{activeRas}]}{[\text{inactiveRas}] \cdot K_{eq}})}{Km_{\text{inactiveRas}} \cdot (1 + \frac{[\text{inactiveRas}]}{Km_{\text{inactiveRas}}} + \frac{[\text{activeRas}]}{Km_{\text{activeRas}}})}](/wiki/images/math/4/6/4/4646fe6671c3abaacf2978b9435be23c.png)
Mass Action
![v_{\text{RasGDPBind}} = k1_{ass} \cdot [\text{RasGDP}] \cdot [\text{Sos}] - k1_{diss} \cdot [\text{RasGDP.Sos}]](/wiki/images/math/1/4/8/148b56226474baac7a16a2f448c65650.png)
![v_{\text{GDPUnbind}} = k2_{ass} \cdot [\text{RasGDP.Sos}] - k2_{diss} \cdot [\text{Ras.Sos}]](/wiki/images/math/9/b/2/9b242880533b0314e145b062060e48d4.png)
![v_{\text{GTPBind}} = k3_{ass} \cdot [\text{Ras.Sos}] - k3_{diss} \cdot [\text{RasGTP.Sos}]](/wiki/images/math/d/3/7/d376dbf56b37975a7eac986b7b2294a4.png)
![v_{\text{RasGTPUnbind}} = k4_{ass} \cdot [\text{RasGTP.Sos}] - k4_{diss} \cdot [\text{RasGTP}] \cdot [\text{Sos}]](/wiki/images/math/c/f/2/cf2cfa91c69930dfef1495dc2cd4ce7f.png)
final Parameter
Michaelis-Menten
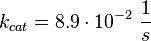
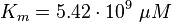
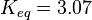
Mass Action
|
1.Step:
2.Step:
|
3.Step:
4.Step:
|
As Michaelis-Menten constants the values by Xu and the averaged relative standard deviation are used:
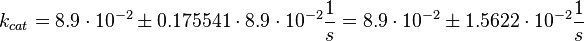
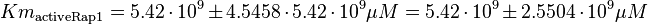
Parameter




The GDP-GTP exchange is modeled as Michaelis-Menten and as binding process.
For the Michaelis-Menten process the kcat and Km values are the same as by Xu et al (2010)[2].
The equilibrium constant is calculated according to the mass action reaction scheme.
The Gibbs free energy of a reaction is:
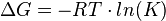 and if the reaction consists of several steps the overall energy is the sum of the individual steps. Therefore the overall equilibrium constant is the product of the indvidual equilibirum constants.
and if the reaction consists of several steps the overall energy is the sum of the individual steps. Therefore the overall equilibrium constant is the product of the indvidual equilibirum constants.
The first step is the binding of RasGDP to Sos.
Figure 2 shows the dissociation rates of three different Ras-isoforms to Sos. The average of the dissociation constants is calculated:
Failed to parse (lexing error): k_{diss_{\text{RasAct_RasGDPBind}}} = \frac{5.6 \cdot 10^{-4} + 6.2 \cdot 10^{-4} + 8.4 \cdot 10^{-4}}{3} \frac{1}{s} = 6.73 \cdot 10^{-4}\ \frac{1}{s}
The corresponding step in the reaction scheme by Lenzen et al. (1998) [1] is step 3 and therefore the equilibrium constant is assumed to be:
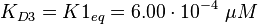 (Fig. 4).
(Fig. 4).
Using the measured dissociation and equilibrium constants the association constant can be calculated Failed to parse (lexing error): (k_{ass} = \frac{k_{diss_{\text{RasAct_RasGDPBind}}}}{K1_{eq}} = 1.12\ \frac{1}{\mu M \cdot s})
.
The second step is the dissociation of GDP.
This is Lenzen et al.'s [1] step four (Fig. 1}).
The equilibrium constant ( K2eq = 8.6 μ M (Fig. 3)) is measured as well as the association rate ( 2.4 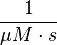 (Fig. 3)). Hence the dissociation rate is calculated as
(Fig. 3)). Hence the dissociation rate is calculated as 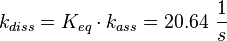 .
.
The third step is the association of GTP.
The calculation is similar to step 2. Equilibrium and association rate are measured [1] ( Keq = 8.4 μM and kass = 2.4 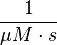 (Fig. 3)) and the dissociation rate is calculated:
(Fig. 3)) and the dissociation rate is calculated:
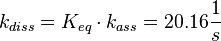 .
.
Because this equation is defined in the other direction 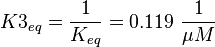 .
.
The fourth step is the unbinding of RasGTP from Sos.
There is no measured equilibrium constant, but one which is derived by a global fit, that is used instead[1] ( 2.00 * 10-4 μM (Fig. 4)). Because of the conformational similarity between GDP and GTP the same dissociation constant as in step 1 is assumed and the association rate is calculated as:
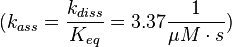 .
.
Because this equation is defined in the other direction 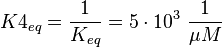
The equilibrium constant is calculated by the product of the four different equilibrium constants:
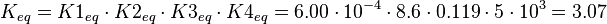
KmP value and equilibrium constant
The Km value for the product is assumed to be similar to but slightly higher than the the Km value of the substrate because of the similarity of the both species. Therefore the Km value of the substrate is multiplied by 1.05 to gain the one of the product and the uncertainty is increased by increasing the error on Kmsubstrate by 50%.
For information about the equilibrium constant please see here.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 C. Lenzen et al. (1998) "Kinetic analysis by fluorescence if the interaction between Ras and the catalytic domain of the guanine nucleotide exchange factor Cdc24Mm." Biochemistry 37.20:7420-7430. DOI 10.1021/bi972621j (pmid:9585556) Cite error: Invalid
<ref>tag; name "Lenzen1998" defined multiple times with different content Cite error: Invalid<ref>tag; name "Lenzen1998" defined multiple times with different content Cite error: Invalid<ref>tag; name "Lenzen1998" defined multiple times with different content - ↑ Xu T. et al. (2010) "Inferring signaling pathway topologies from multiple perturbation measurements of specific biochemical species." Sci Signal. 3(134):ra20. (pmid:20234003)