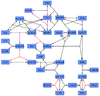
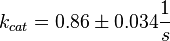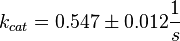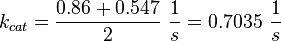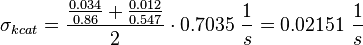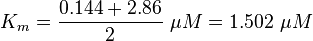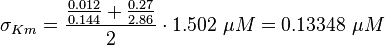ERK-Inactivation
Reaction
Step 1:
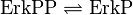
Step 2:
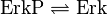
Rate Equation
Step 1:
Step 2:
final Parameter
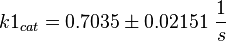
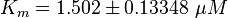
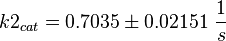
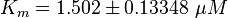
Parameter
| Notes | References |
|---|---|
|
Calculation of kcat Dephosphorylation by HePTP
Dephosphorylation by MKP
Averaging
Calculation of Km Averaging
|
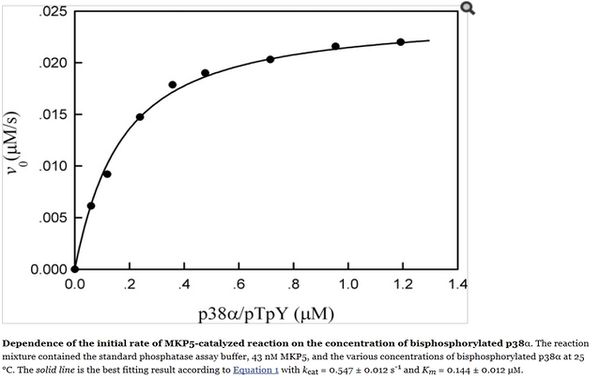 Zhang Y. et al (2008)[1]  Zhang Y. et al (2008)[1] |
Background Information
There are several phosphatases which dephosphorylate ERK, among them phosphatase 2A (PP2A), MAPK phosphatase 3, HePTP and protein phosphatase-1 (PP1). [2] [3] [4] [5] PP2A is more effective than PP1 [3] and it is used by Brown KS and Sethan JP [6] in their model. Xu et al. 2010 [7] based theit model on this model and also elicit their initial conditions from this model. We introduced PP2A in our model to use the measured kcat values and our initial concentration we elicit form Brown and Sethan [6] in a similar way to Xu et al. [7] so that the relation of the concentrations is concerved.
KmP value and equilibrium constant
The Km value for the product is assumed to be similar but slightly higher than the the Km value of the substrate because of the similarity of the both species. Therefore the Km value of the substrate is multiplied by 1.05 to gain the one of the product and the uncertainty is increased by increasing the error on Kmsubstrate by 50%.
For information about the equilibrium constant please see here.
References
- ↑ 1.0 1.1 Zhang Y. et al (2008) Enzymatic Activity and Substrate Specificity of Mitogen-activated Protein Kinase p38α in Different Phosphorylation Sites, J.Biol.Chem.;283,26591-2660f (pmid:18669639) Cite error: Invalid
<ref>tag; name "Zhang2008" defined multiple times with different content - ↑ Li R., Gong Z., Pan C., Xie DD., Tang JY., et al. (2013) Metal-dependent protein phosphatase 1a functions as an extracellular signal-regulated kinase phosphatase. FEBS J 280:2700-2711 (pmid:23560844)
- ↑ 3.0 3.1 Alessi DR, Gomez N, Moorhead G, Lewis T, Keyse SM, Cohen P. (1995) Inactivation of p42 MAP kinase by protein phosphatase 2A and a protein tyrosine phosphatase, but not CL100, in various cell lines. Curr Biol. 5(3):283-95. (pmid:7780739)
- ↑ Anderson NG, Maller JL, Tonks NK, Sturgill TW. (1990) Requirement for integration of signals from two distinct phosphorylation pathways for activation of MAP kinase. Nature 343(6259):651-3.(pmid:2154696)
- ↑ Sontag E, Fedorov S, Kamibayashi C, Robbins D, Cobb M, Mumby M. (1993) The interaction of SV40 small tumor antigen with protein phosphatase 2A stimulates the map kinase pathway and induces cell proliferation. Cell 75(5):887-97. (pmid:8252625)
- ↑ 6.0 6.1 Brown KS, Sethan JP (2003) Statistical mechanical approaches to models with many poorly known parameters. Phys Rev E Stat Nonlin Soft Matter Phys 68: 021904
- ↑ 7.0 7.1 Tian-Rui Xu et al. (2010) "Inferring signaling pathway topologies from multiple perturbation measurements of specific biochemical species." Sci Signal. 3(134):ra20. (pmid:20234003)