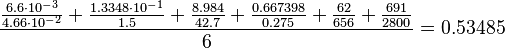Calculation of the averaged relative error
Equilibrium constant
The only steps for which an error on the equilibrium constant is really measured is the phosphorylation by creatine kinase and the activation of C3G Therefore this relative error is calculated and assumed as relative error for the reactions for which no hint about the uncertainty is given in the literature. (Reactions are: Ras-Activation and Inactivation as well as Rap1-Activation and Inactivation)
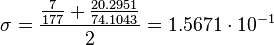
Assoziation
There are experimental errors on the binding of EGF to EGFR and of Sos to EGFR. The relative error of these two reactions is averaged.
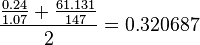
Dissoziation
There are experimental errors on the binding of EGF to EGFR and of Sos to EGFR. The relative error of these two reactions is averaged.
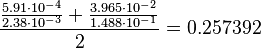
kcat
For the calculation of the averaged relative error six reactions are taken into account (both Erk-Inactivation steps, Mek-Activation(BRaf), Raf1-Removal and both Sos-Removal steps).
For the Mek-activation and Raf1-Removal process, the actual relative error without any further transformation is used.
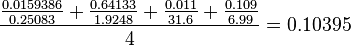
Km
The same reaction as for kcat are taken into account, plus the second step of the Erk-Activation process.