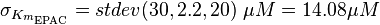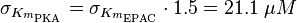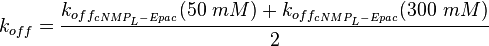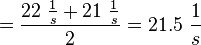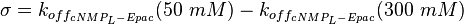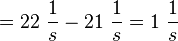EPAC and PKA-Activation (Agonist)

-> back to the overview

The EPAC and PKA-Activation is modelled in two different ways. Once to keep as close as possible to Xu et al. (2010) following Michaelis-Menten kinetics (non-modified model) and once as mass action kinetics (modified model), because the activation of those molecules is not due to an enzymatic catalysation but due to binding of cAMP (Kraemer A. et al. 2001).

Binding Reaction

$\text{inactiveEPAC} + \text{agonist} \rightleftharpoons \text{activeEPAC} + \text{agonist}$

$\text{inactivePKA} + \text{agonist} \rightleftharpoons \text{activePKA} + \text{agonist}$

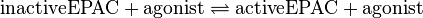
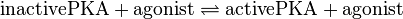
Kinetic Equation

$v_{\text{EPAC-Activation}}=\frac{k_{cat} \cdot [\text{agonist}] \cdot [\text{inactiveEPAC}] \cdot (1-\frac{[\text{activeEPAC}]}{[\text{inactiveEPAC}] \cdot K_{eq}})}{Km_{\text{inactiveEPAC}} \cdot (1 + \frac{[\text{inactiveEPAC}]}{Km_{\text{inactiveEPAC}}} + \frac{[\text{activeEPAC}]}{Km_{\text{activeEPAC}}})}$

$v_{\text{PKA-Activation}}=\frac{k_{cat} \cdot [\text{agonist}] \cdot [\text{inactivePKA}] \cdot (1-\frac{[\text{activePKA}]}{[\text{inactivePKA}] \cdot K_{eq}})}{Km_{\text{inactiveEPAC}} \cdot (1 + \frac{[\text{inactivePKA}]}{Km_{\text{inactivePKA}}} + \frac{[\text{activePKA}]}{Km_{\text{activePKA}}})}$

final Parameter

Michaelis-Menten:

$K_{m_{\text{EPAC}}} = 17.4 \pm 14.1\ \mu M$

$K_{m_{\text{PKA}}} = 17.4 \pm 14.1 \cdot 1.5\ \mu M = 17.4 \pm 21.1\ \mu M$

$K_{cat_{\text{EPAC}}} = 4.07534\ \frac{1}{s}$

$K_{cat_{\text{PKA}}} = 1.20102\ \frac{1}{s}$

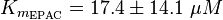
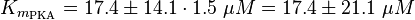
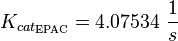
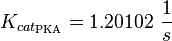
Binding reaction:

$k_{on_{\text{EPAC}}} = 15 \pm 5.6\ \frac{1}{\mu M \cdot s}$

$k_{off{\text{EPAC}}} = 21.5 \pm 1\ \frac{1}{s}$

$k_{on_{\text{PKA}}} = 15 \pm 5.6\cdot 1.5 \frac{1}{\mu M \cdot s} = 15 \pm 8.4\ \frac{1}{\mu M \cdot s}$

$k_{off{\text{PKA}}} = 21.5 \pm 1\cdot 1.5 \frac{1}{s} = 21.5 \pm 1.5\ \frac{1}{s}$

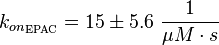
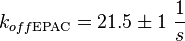
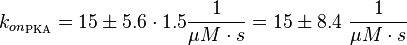
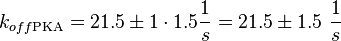
Parameter Annotations

Notes	References
To calculate the Km values for EPAC and PKA the average of three measured values is used. The Km value for the activation by cAMP is measured twice and the activation by 8CPT-2Me-cAMP once. Because this reaction is included in our model to increase comparability with Xu et al's model and they used this analogon for their measurements all three values are averaged. The values are: KmcAMP(EPAC1) = 30 μM; Enserink et al.(2002) Km8CPT-2Me-cAMP(EPAC1) = 2.2 μM; Enserink et al. (2002) KmcAMP(EPAC2) = 20 μM; Rehmann H. et al. (2008) There are no measured values for the PKA activation by cAMP. However it can be assumed that the values are similar to the ones for EPAC activation. Therefore the same value as for EPAC activation is used and the assumed error is the error used for EPAC activation increased by 50%, because the reaction is not the reaction measured. Calculation Failed to parse (lexing error): K_{m_{\text{EPAC & PKA}}} = \frac{30\; \mu M + 2.2\; \mu M + 20\; \mu M}{3} = 17.4\; \mu M $\sigma_{K_{m_{\text{EPAC}}}} = stdev(30, 2.2, 20)\; \mu M = 14.08 \mu M$ $\sigma_{K_{m_{\text{PKA}}}} = \sigma_{K_{m_{\text{EPAC}}}} \cdot 1.5 = 21.1\; \mu M$	Enserink et al.(2002) Rehmann H. et al. (2008); Supplementary
The kcat values by Xu et al. (2010) are used and to estimate the error the relative errors of all measured kcat values used in this model are averaged and this value is assumed to be the relative error of this kcat value. (Calculation of the averaged relative error)
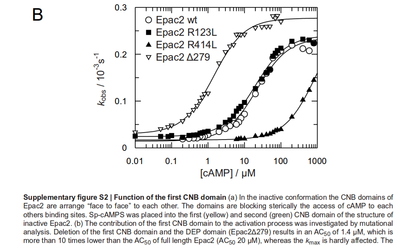
It is shown, that the catalytic domain of EPAC has no influence on the binding ability of EPAC concerning cAMP (Kraemer et al., 2001). Binding experiment between the cAMP-binding domain (cNMPL-EPAC) and cAMP were performed at two different NaCl-level. The dissociation rate differs only slightly, whereas the association rate seems to be dependent on the NaCl-level. The intracellular sodium concentration in E.coli varies between 5-14 mM (Lo et al. 2006) and can therefore be assumed as less than 50 mM. Calculation of the kon: Due to the fact that there are only two values measured, no assumption can be made about the function which describes the relation between the sodium concentration and the association constant. However at higher sodium concentrations a decrease of kon was observed and this justifies the assumption that at lower sodium concentrations the association rate might be even higher. It might however be the other way round as well, because possibly the peak of the function is at 50 mM NaCl. We assume that the true value at an intracellular NaCl concentration <50mM is slightly higher than the value measured at 50mM, so the mean of kon is set to 15 1/μMs. To estimate the uncertainty of this parameter the difference between the two measured values is set to σ. Calculation of the koff: The two values differ only sightly, so we assume that the dissociation rate does not depend on the sodium concentration. Therefore the two values are averaged to get the mean and the error is estimated similar to kon. The measured values are: koncNMP_L-Epac = 14.4 1/μMs; 50 mM NaCl (Kraemer et al., 2001) koncNMP_L-Epac= 8.8 1/μMs; 300 mM NaCl (Kraemer et al., 2001) koffcNMP_L-Epac = 22 s-1; 50 mM NaCl (Kraemer et al., 2001) koffcNMP_L-Epac = 21 s-1; 300 mM NaCl (Kraemer et al., 2001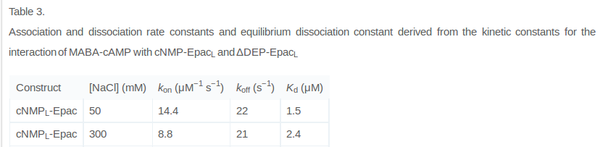)	Kraemer et al. (2001) Calculation koff: average: $k_{off} = \frac{k_{off_{cNMP_L-Epac}}(50\ mM)+k_{off_{cNMP_L-Epac}}(300\ mM)}{2}$ $=\frac{22\ \frac{1}{s} + 21\ \frac{1}{s}}{2} = 21.5\ \frac{1}{s}$ uncertainty: $\sigma = k_{off_{cNMP_L-Epac}}(50\ mM) - k_{off_{cNMP_L-Epac}}(300\ mM)$ $= 22\ \frac{1}{s} - 21\ \frac{1}{s} = 1\ \frac{1}{s}$

Km_P value and equilibrium constant

The K_m value for the product is assumed to be similar but slightly higher than the the K_m value of the substrate because of the similarity of the both species. Therefore the K_m value of the substrate is multiplied by 1.05 to gain the one of the product and the uncertainty is increased by increasing the error on Km_substrate by 50%.

For information about the equilibrium constant please see here.