Difference between revisions of "Mitocondrial pyruvate metabolism"
(→Rate equation) |
|||
| Line 8: | Line 8: | ||
==Rate equation== | ==Rate equation== | ||
*Chemical reactions proceed to equilibrium within closed systems. For a simple reaction <math>A \rightarrow B</math> it is defined as <math>K_{eq} = \frac{[B]_{eq}}{[A]_{eq}}</math> where forward and reverse rates are equal. | *Chemical reactions proceed to equilibrium within closed systems. For a simple reaction <math>A \rightarrow B</math> it is defined as <math>K_{eq} = \frac{[B]_{eq}}{[A]_{eq}}</math> where forward and reverse rates are equal. | ||
| − | *Equilibrium is not reached in open system due to influx and outflux. '''Mass action ratio''' <math>\ | + | *Equilibrium is not reached in open system due to influx and outflux. '''Mass action ratio''' <math>\Tau</math> for <math>A \rightarrow B</math> reaction is defined as <math>\tau = \frac{[B]_{ob}}{[A]_{ob}}</math> where subscript ''ob'' represents observable at a given point. |
Constant flux is used where <math> v = 1 \times 10^{-4}</math> is considered. | Constant flux is used where <math> v = 1 \times 10^{-4}</math> is considered. | ||
Revision as of 10:17, 12 May 2014
Mitocondrial pyruvate metabolism(MPM) is an enzyme that generates ATP form pyruvate.
Chemical reaction
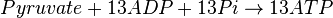
Rate equation
- Chemical reactions proceed to equilibrium within closed systems. For a simple reaction
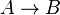 it is defined as
it is defined as ![K_{eq} = \frac{[B]_{eq}}{[A]_{eq}}](/wiki/images/math/a/c/8/ac844b70f8f7c5f1d91accb00061a1ea.png) where forward and reverse rates are equal.
where forward and reverse rates are equal. - Equilibrium is not reached in open system due to influx and outflux. Mass action ratio Failed to parse (Cannot store math image on filesystem.): \Tau
for
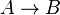 reaction is defined as
reaction is defined as ![\tau = \frac{[B]_{ob}}{[A]_{ob}}](/wiki/images/math/8/0/5/8050a810298db95df036d87c2e79f1ea.png) where subscript ob represents observable at a given point.
where subscript ob represents observable at a given point.
Constant flux is used where 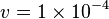 is considered.
is considered.
Parameter values
| Parameter | Value | Organism | Remarks |
|---|---|---|---|
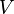
|
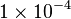 [1] [1]
|
HeLa cell line | Constant flux |