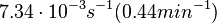Difference between revisions of "Binding of A-R2 to OA' operator"
(→Parameters with uncertainty) |
(→Parameters) |
||
| (24 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{DISPLAYTITLE: Binding of | + | {{DISPLAYTITLE: Binding of AR<sub>2</sub> to OA' operator}} |
| − | The ScbA-ScbR complex (AR<sub>2</sub>) binds to the | + | The ScbA-ScbR complex (AR<sub>2</sub>) binds to the putative ScbA gene operator (O<sub>A</sub>') and activates its maximum mRNA transcription. In the model, O<sub>A</sub> and O<sub>A</sub>' are considered together under the general name O<sub>A</sub> which can be found at different states. When only AR<sub>2</sub> is bound, maximum transcription is activated. When both AR<sub>2</sub> and R<sub>2</sub> or two R<sub>2</sub>s are bound, the promoter is repressed. The different statuses of the promoter are represented by the set of reactions below. |
<imagemap> | <imagemap> | ||
Image:Back button.png|150px|right|alt=Go back to overview | Image:Back button.png|150px|right|alt=Go back to overview | ||
| Line 8: | Line 8: | ||
==Chemical equation== | ==Chemical equation== | ||
| − | <center><math>O_{A} | + | <center><math>O_{A} + AR_{2} \rightleftharpoons O_{A}-AR_{2}</math></center> |
| + | |||
| + | <center><math>O_{A}-R_{2} + AR_{2} \rightleftharpoons O_{A}-R_{2}-AR_{2}</math></center> | ||
| + | |||
| + | <center><math>O_{A}-2R_{2} + AR_{2} \rightleftharpoons O_{A}-2R_{2}-AR_{2}</math></center> | ||
| + | |||
| + | <center><math>O_{A}-AR_{2} + R_{2} \rightleftharpoons O_{A}-R_{2}-AR_{2}</math></center> | ||
| + | |||
| + | <center><math>O_{A}-R_{2}-AR_{2} + R_{2} \rightleftharpoons O_{A}-2R_{2}-AR_{2}</math></center> | ||
== Rate equation == | == Rate equation == | ||
| − | <center><math> | + | <center><math> r1= \frac{k^{-}_{5}}{K_{d5}}\cdot [O_{A}]\cdot [AR_{2}] - k^{-}_{5}\cdot [O_{A}-AR_{2}]</math></center> |
| + | |||
| + | <center><math> r2= \frac{k^{-}_{9}}{K_{d9}}\cdot [O_{A}-R_{2}]\cdot [AR_{2}] - k^{-}_{9}\cdot [O_{A}-R_{2}-AR_{2}]</math></center> | ||
| + | |||
| + | <center><math> r3= \frac{k^{-}_{10}}{K_{d10}}\cdot [O_{A}-2R_{2}]\cdot [AR_{2}] - k^{-}_{10}\cdot [O_{A}-2R_{2}-AR_{2}]</math></center> | ||
| + | |||
| + | <center><math> r4= \frac{k^{-}_{11}}{K_{d11}}\cdot [O_{A}-AR_{2}]\cdot [R_{2}] - k^{-}_{11}\cdot [O_{A}-R_{2}-AR_{2}]</math></center> | ||
| + | |||
| + | <center><math> r5= \frac{k^{-}_{12}}{K_{d12}}\cdot [O_{A}-R_{2}-AR_{2}]\cdot [R_{2}] - k^{-}_{12}\cdot [O_{A}-2R_{2}-AR_{2}]</math></center> | ||
== Parameters == | == Parameters == | ||
| − | The parameters of | + | The parameters of the reaction of the AR<sub>2</sub> complex binding to the putative promoter are the dissociation constant for binding of ScbA-ScbR to O<sub>A</sub>' (<math>K_{d5}</math>) and the dissociation rate for binding of ScbA-ScbR to O<sub>A</sub>' (<math>k^{-}_{5}</math>). The parameters for the other reactions will have the same distributions, as they refer to a similar binding process and by taking uncertainty into account, the range of parameter values can be considered the same. Therefore, <math>K_{d9}</math>, <math>K_{d10}</math>, <math>K_{d11}</math> and <math>K_{d12}</math> will follow the same distribution as <math>K_{d5}</math> and <math>k^{-}_{9}</math>, <math>k^{-}_{10}</math>, <math>k^{-}_{11}</math> and <math>k^{-}_{12}</math> will follow the same distribution as <math>k^{-}_{5}</math>. |
| + | |||
| + | Since there is no evidence of the actual existence of the ScbA-ScbR complex, we assumed that its binding affinity for the O<sub>A</sub> operator would follow a similar behaviour to the binding of ScbR to O<sub>R</sub>. ScbR is a member of the TetR family of repressors, named after the member of this group which is the most completely characterized, the TetR repressor protein. TetR binds to the operator tetO, repressing its own expression and that of the efflux determinant tetA in a similar way as ScbR binding to O<sub>R</sub> and O<sub>A</sub> and repressing its own expression and the expression of ScbA. Therefore parameter values were derived from published data on the TetR-tetO interaction and on tetR-like proteins binding to their corresponding operators. | ||
{|class="wikitable" | {|class="wikitable" | ||
| Line 26: | Line 44: | ||
|- | |- | ||
|<math>K_{d5}</math> | |<math>K_{d5}</math> | ||
| + | <math>K_{d9}</math> | ||
| + | <math>K_{d10}</math> | ||
| + | <math>K_{d11}</math> | ||
| + | <math>K_{d12}</math> | ||
|<math>0.005 - 5.8 </math> <ref name="Kleinschmidt1988"> [http://pubs.acs.org/doi/pdf/10.1021/bi00404a003 Kleinschmidt C., Tovar K., Hillen W., Porschke D. ''Dynamics of repressor-operator recognition: Tn10-encoded tetracycline resistance control.'' Biochemistry, 1988, 27(4), pp. 1094–1104.]</ref> <ref name="Kamionka2004"> [http://www.ncbi.nlm.nih.gov/pmc/articles/PMC373327/pdf/gkh200.pdf Kamionka A, Bogdanska-Urbaniak J, Scholz O, Hillen W. ''Two mutations in the tetracycline repressor change the inducer anhydrotetracycline to a corepressor.'' Nucleic Acids Research. 2004;32(2):842-847.]</ref> <ref name="Bolla2012"> [http://nar.oxfordjournals.org/content/40/18/9340.full-text-lowres.pdf Bolla JR, Do SV, Long F, et al. ''Structural and functional analysis of the transcriptional regulator Rv3066 of Mycobacterium tuberculosis.'' Nucleic Acids Research. 2012;40(18):9340-9355.] </ref> <ref name="Ahn2007"> [http://jb.asm.org/content/189/18/6655.full.pdf Ahn SK, Tahlan K, Yu Z, Nodwell J. ''Investigation of Transcription Repression and Small-Molecule Responsiveness by TetR-Like Transcription Factors Using a Heterologous Escherichia coli-Based Assay.'' Journal of Bacteriology. 2007;189(18):6655-6664.]</ref> | |<math>0.005 - 5.8 </math> <ref name="Kleinschmidt1988"> [http://pubs.acs.org/doi/pdf/10.1021/bi00404a003 Kleinschmidt C., Tovar K., Hillen W., Porschke D. ''Dynamics of repressor-operator recognition: Tn10-encoded tetracycline resistance control.'' Biochemistry, 1988, 27(4), pp. 1094–1104.]</ref> <ref name="Kamionka2004"> [http://www.ncbi.nlm.nih.gov/pmc/articles/PMC373327/pdf/gkh200.pdf Kamionka A, Bogdanska-Urbaniak J, Scholz O, Hillen W. ''Two mutations in the tetracycline repressor change the inducer anhydrotetracycline to a corepressor.'' Nucleic Acids Research. 2004;32(2):842-847.]</ref> <ref name="Bolla2012"> [http://nar.oxfordjournals.org/content/40/18/9340.full-text-lowres.pdf Bolla JR, Do SV, Long F, et al. ''Structural and functional analysis of the transcriptional regulator Rv3066 of Mycobacterium tuberculosis.'' Nucleic Acids Research. 2012;40(18):9340-9355.] </ref> <ref name="Ahn2007"> [http://jb.asm.org/content/189/18/6655.full.pdf Ahn SK, Tahlan K, Yu Z, Nodwell J. ''Investigation of Transcription Repression and Small-Molecule Responsiveness by TetR-Like Transcription Factors Using a Heterologous Escherichia coli-Based Assay.'' Journal of Bacteriology. 2007;189(18):6655-6664.]</ref> | ||
| <math>nM</math> | | <math>nM</math> | ||
| Line 35: | Line 57: | ||
[[Image:Kd1-text3.png|center|thumb|350px|Kleinschmidt et al. 1988<ref name="Kleinschmidt1988"></ref>]] | [[Image:Kd1-text3.png|center|thumb|350px|Kleinschmidt et al. 1988<ref name="Kleinschmidt1988"></ref>]] | ||
| − | Data derived from equilibrium SPR analysis of TetR-tetO interaction report a K<sub>a</sub> of <math>5.6 \pm 2 nM^{-1}</math><ref name="Kamionka2004"></ref>, therefore a K<sub>d</sub> (<math>\frac{1}{K_a}</math>) of <math>0.179 \pm 0. | + | Data derived from equilibrium SPR analysis of TetR-tetO interaction report a K<sub>a</sub> of <math>5.6 \pm 2 nM^{-1}</math><ref name="Kamionka2004"></ref>, therefore a K<sub>d</sub> (<math>\frac{1}{K_a}</math>) of <math>0.179 \pm 0.064 nM</math>. ''E. coli'' was used as a host for the expression of proteins and the experiments were conducted with synthetic tetO-containing fragments. |
[[Image:Kd1-table1.png|center|thumb|600px|Kamionka et al. 2004 <ref name="Kamionka2004"></ref>]] | [[Image:Kd1-table1.png|center|thumb|600px|Kamionka et al. 2004 <ref name="Kamionka2004"></ref>]] | ||
| Line 46: | Line 68: | ||
|- | |- | ||
|<math>k^{-}_{5}</math> | |<math>k^{-}_{5}</math> | ||
| − | |<math>0.09- | + | |
| + | <math>k^{-}_{9}</math> | ||
| + | |||
| + | <math>k^{-}_{10}</math> | ||
| + | |||
| + | <math>k^{-}_{11}</math> | ||
| + | |||
| + | <math>k^{-}_{12}</math> | ||
| + | |||
| + | |<math>0.09-0.846</math> <ref name="Kleinschmidt1988"></ref> <ref name="Li2012"> [http://aem.asm.org/content/78/17/6009.full.pdf Li T, Zhao K, Huang Y, et al. ''The TetR-Type Transcriptional Repressor RolR from Corynebacterium glutamicum Regulates Resorcinol Catabolism by Binding to a Unique Operator, rolO.'' Applied and Environmental Microbiology. 2012;78(17):6009-6016.] </ref> | ||
|<math>min^{-1}</math> | |<math>min^{-1}</math> | ||
|N/A | |N/A | ||
| Line 56: | Line 87: | ||
[[Image:K1-text.png|center|thumb|400px|Li et al. 2012<ref name="Li2012"></ref>]] | [[Image:K1-text.png|center|thumb|400px|Li et al. 2012<ref name="Li2012"></ref>]] | ||
| − | As less information was available for <math>k^{-}_{5}</math>, most of which was acquired by ''in vitro'' measurements and none was derived from ''Streptomyces'', | + | As less information was available for <math>k^{-}_{5}</math>, most of which was acquired by ''in vitro'' measurements and none was derived from ''Streptomyces'', the uncertainty associated with this parameter is larger and should be taken into account while designing the corresponding distributions. |
|} | |} | ||
==Parameters with uncertainty== | ==Parameters with uncertainty== | ||
| − | When deciding how to describe the uncertainty for each parameter there are a few points to be taken into consideration. Firstly, the values reported in literature are spread in a relatively large range and correspond to different protein-operator binding reactions, although all are part of the same family of repressors (TetR). Additionally, the values were acquired by ''in vitro'' testing, although in some of the publications a strong correlation between ''in vitro'' and ''in vivo'' measurements is noted. This means that there might be a notable difference between actual parameter values and the ones reported in literature. | + | When deciding how to describe the uncertainty for each parameter there are a few points to be taken into consideration. Firstly, the values reported in literature are spread in a relatively large range and correspond to different protein-operator binding reactions, although all are part of the same family of repressors (TetR). Additionally, the values were acquired by ''in vitro'' testing, although in some of the publications a strong correlation between ''in vitro'' and ''in vivo'' measurements is noted. This means that there might be a notable difference between actual parameter values and the ones reported in literature. These facts influence the weight assigned to each parameter value, the quantification of the parameter uncertainty and therefore the shape of the corresponding distributions. Therefore, by assigning the appropriate weights to the parameter values and using the method described [[Quantification of parameter uncertainty#Design of probability distributions|'''here''']], the appropriate probability distributions were designed. |
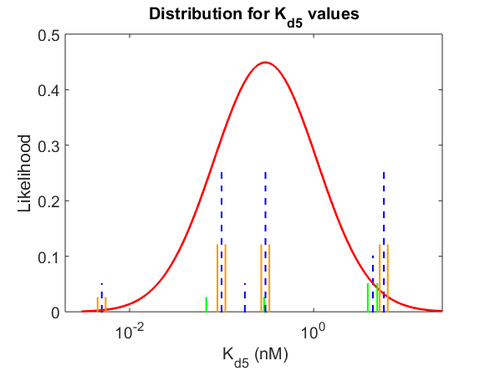
| + | |||
| + | More specifically, with regards to the <math>K_{d5}</math>, the value that is considered as the most accurate in different publications is <math> 0.005 nM </math> measured by Kleinschmidt et al. However, the K<sub>d</sub> s measured for the ActR protein in ''S. coelicolor'' cover the range of <math> 0.1-5.8 nM </math>. Therefore, the mode of the log-normal distribution calculated for the <math>K_{d5}</math> is <math> 0.299 nM </math> which is within the range of the values reported for ''S. coelicolor'' and the Spread is <math> 6.8 </math> in order to be able to explore a wide range of values and thus take into account the uncertainty caused by both the ''in vitro'' testing and the measurements in different species and proteins. Thus, the range where 68.27% of the values are found is between 0.044 and 2.048 nM. | ||
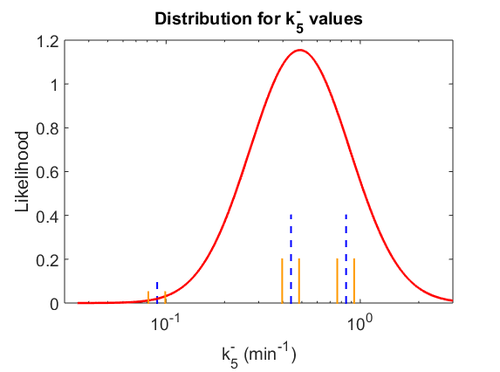
| − | + | Similarly, the value calculated for the <math>k^{-}_{5}</math> by the measurements of Kleinschmidt et al. is <math>0.09 min^{-1}</math>, however other studies reported values of up to <math>0.85 min^{-1}</math>. After considering all the factors and assigning the relevant weights to the parameter values, the mode of the log-normal distribution calculated for <math>k^{-}_{5}</math> was <math>0.489 min^{-1}</math> and the Spread was <math>1.98</math>. This means that the range where 68.27% of the values are found is between 0.247 and 0.968 <math>min^{-1}</math>. | |
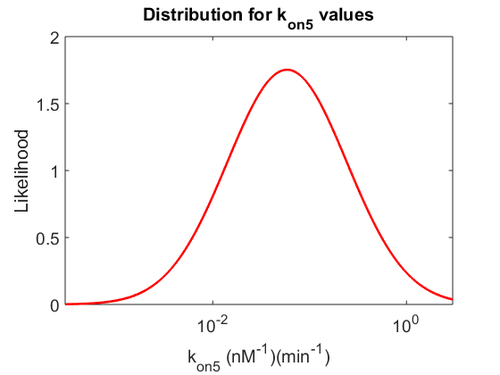
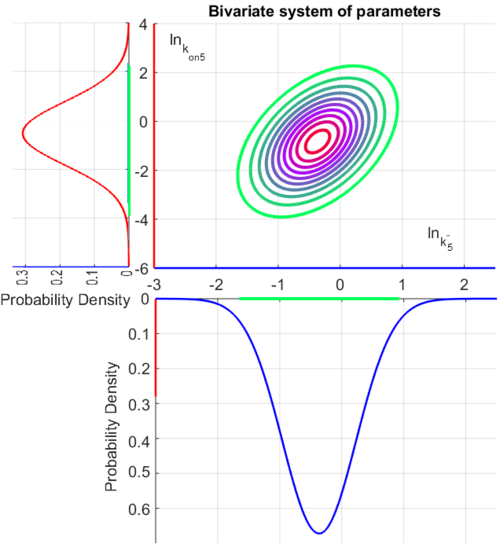
| − | + | Since the two parameters are interdependent, thermodynamic consistency also needs to be taken into account. This is achieved by creating a bivariate system as described [[Quantification of parameter uncertainty#Parameter dependency and thermodynamic consistency|'''here''']]. Since <math>k_{on5}</math> is the parameter with the largest geometric coefficient of variation, as only one reported value was retrieved from literature, this is set as the dependent parameter as per: <math>k_{on5}=\frac{k^{-}_{5}}{k_{d5}}</math>. The location and scale parameters of <math>k_{on5}</math> (μ=-0.53113 and σ=1.3034) were calculated from those of <math>K_{d5}</math> and <math>k^{-}_{5}</math>. | |
| − | + | The probability distributions for the three parameters, adjusted accordingly in order to reflect the above values, are the following: | |
| − | The probability distributions for the | ||
| − | [[Image: | + | [[Image:KD5u.png|500px]] [[Image:K5u.png|500px]] [[Image:Kon5u.png|500px]] |
| − | The correlation matrix which is necessary to define the relationship between the two marginal distributions (<math>k_{on5}</math>,<math>k^{-}_{5}</math>) of the bivariate system is derived by employing random values generated by the two distributions. | + | The values retrieved from literature and their weights are indicated by the blue dashed lines, and the uncertainty for each value is indicated using the reported experimental error (green lines) or a default value of 10% error (orange lines). The correlation matrix which is necessary to define the relationship between the two marginal distributions (<math>k_{on5}</math>,<math>k^{-}_{5}</math>) of the bivariate system is derived by employing random values generated by the two distributions. |
| − | The | + | The parameter information of the distributions of the multivariate system is: |
{|class="wikitable" | {|class="wikitable" | ||
! Parameter | ! Parameter | ||
| + | ! Mode | ||
| + | ! Spread | ||
! μ | ! μ | ||
! σ | ! σ | ||
| Line 82: | Line 116: | ||
|- | |- | ||
|<math>K_{d5}</math> | |<math>K_{d5}</math> | ||
| − | |<math> | + | |<math>0.299</math> |
| − | |<math>1. | + | |<math>6.8</math> |
| + | |<math>0.15471</math> | ||
| + | |<math>1.1661</math> | ||
|N/A | |N/A | ||
|- | |- | ||
|<math>k^{-}_{5}</math> | |<math>k^{-}_{5}</math> | ||
| − | |<math>-0. | + | |<math>0.489</math> |
| − | |<math>0. | + | |<math>1.98</math> |
| − | |rowspan="2"|<math>\begin{pmatrix} 1 & 0. | + | |<math>-0.37642</math> |
| − | 0. | + | |<math>0.58225</math> |
| + | |rowspan="2"|<math>\begin{pmatrix} 1 & 0.3045 \\ | ||
| + | 0.3045 & 1 \end{pmatrix}</math> | ||
|- | |- | ||
|<math>k_{on5}</math> | |<math>k_{on5}</math> | ||
| − | |<math>-0. | + | |N/A |
| − | |<math>1. | + | |N/A |
| + | |<math>-0.53113</math> | ||
| + | |<math>1.3034</math> | ||
|} | |} | ||
The multivariate system of the normal distributions (<math>ln(k^{-}_{5})</math> and <math>ln(k_{on5})</math>) and the resulting samples of values are presented in the following figure: | The multivariate system of the normal distributions (<math>ln(k^{-}_{5})</math> and <math>ln(k_{on5})</math>) and the resulting samples of values are presented in the following figure: | ||
| − | [[Image:Multidist5.png| | + | [[Image:Multidist5.png|500px]] |
In this way, a system of distributions is created where each distribution is described and constrained by the other two. Therefore, the parameters will be sampled by the two marginal distributions in a way consistent with our beliefs and with the relevant thermodynamic constraints. However, since the model's reaction rate requires the parameters <math>K_{d5}</math> and <math>k^{-}_{5}</math>, and not the <math>k_{on5}</math>, the value for <math>K_{d5}</math> is calculated by the parameters sampled from the other two distributions in an additional step, as per <math>k_{d5}=\frac{k^{-}_{5}}{k_{on5}}</math>. | In this way, a system of distributions is created where each distribution is described and constrained by the other two. Therefore, the parameters will be sampled by the two marginal distributions in a way consistent with our beliefs and with the relevant thermodynamic constraints. However, since the model's reaction rate requires the parameters <math>K_{d5}</math> and <math>k^{-}_{5}</math>, and not the <math>k_{on5}</math>, the value for <math>K_{d5}</math> is calculated by the parameters sampled from the other two distributions in an additional step, as per <math>k_{d5}=\frac{k^{-}_{5}}{k_{on5}}</math>. | ||
| + | All the above apply as well for the parameters <math>K_{d9}</math>, <math>K_{d10}</math>, <math>K_{d11}</math>, <math>K_{d12}</math>, <math>k^{-}_{9}</math>, <math>k^{-}_{10}</math>, <math>k^{-}_{11}</math> and <math>k^{-}_{12}</math>. | ||
==References== | ==References== | ||
<references/> | <references/> | ||
Latest revision as of 17:42, 4 January 2018
The ScbA-ScbR complex (AR2) binds to the putative ScbA gene operator (OA') and activates its maximum mRNA transcription. In the model, OA and OA' are considered together under the general name OA which can be found at different states. When only AR2 is bound, maximum transcription is activated. When both AR2 and R2 or two R2s are bound, the promoter is repressed. The different statuses of the promoter are represented by the set of reactions below.
Contents
Chemical equation
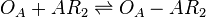
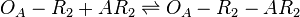
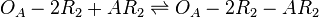
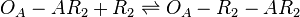
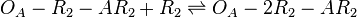
Rate equation
![r1= \frac{k^{-}_{5}}{K_{d5}}\cdot [O_{A}]\cdot [AR_{2}] - k^{-}_{5}\cdot [O_{A}-AR_{2}]](/wiki/images/math/5/2/3/523ce82eeedb646abbc55fdf7ca9c7ee.png)
![r2= \frac{k^{-}_{9}}{K_{d9}}\cdot [O_{A}-R_{2}]\cdot [AR_{2}] - k^{-}_{9}\cdot [O_{A}-R_{2}-AR_{2}]](/wiki/images/math/e/0/8/e08d9b67d11a077b156a521045ea7eb5.png)
![r3= \frac{k^{-}_{10}}{K_{d10}}\cdot [O_{A}-2R_{2}]\cdot [AR_{2}] - k^{-}_{10}\cdot [O_{A}-2R_{2}-AR_{2}]](/wiki/images/math/c/b/d/cbd1812d397dbc4b9fb2754ebef289e4.png)
![r4= \frac{k^{-}_{11}}{K_{d11}}\cdot [O_{A}-AR_{2}]\cdot [R_{2}] - k^{-}_{11}\cdot [O_{A}-R_{2}-AR_{2}]](/wiki/images/math/1/8/f/18fa33239bd87858445fc5b18f0f5060.png)
![r5= \frac{k^{-}_{12}}{K_{d12}}\cdot [O_{A}-R_{2}-AR_{2}]\cdot [R_{2}] - k^{-}_{12}\cdot [O_{A}-2R_{2}-AR_{2}]](/wiki/images/math/6/7/1/6717daee0174505fba61b7649ed819f8.png)
Parameters
The parameters of the reaction of the AR2 complex binding to the putative promoter are the dissociation constant for binding of ScbA-ScbR to OA' (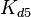 ) and the dissociation rate for binding of ScbA-ScbR to OA' (
) and the dissociation rate for binding of ScbA-ScbR to OA' (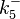 ). The parameters for the other reactions will have the same distributions, as they refer to a similar binding process and by taking uncertainty into account, the range of parameter values can be considered the same. Therefore,
). The parameters for the other reactions will have the same distributions, as they refer to a similar binding process and by taking uncertainty into account, the range of parameter values can be considered the same. Therefore, 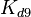 ,
, 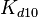 ,
, 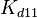 and
and 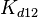 will follow the same distribution as
will follow the same distribution as 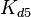 and
and 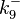 ,
, 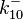 ,
, 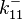 and
and 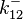 will follow the same distribution as
will follow the same distribution as 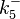 .
.
Since there is no evidence of the actual existence of the ScbA-ScbR complex, we assumed that its binding affinity for the OA operator would follow a similar behaviour to the binding of ScbR to OR. ScbR is a member of the TetR family of repressors, named after the member of this group which is the most completely characterized, the TetR repressor protein. TetR binds to the operator tetO, repressing its own expression and that of the efflux determinant tetA in a similar way as ScbR binding to OR and OA and repressing its own expression and the expression of ScbA. Therefore parameter values were derived from published data on the TetR-tetO interaction and on tetR-like proteins binding to their corresponding operators.
| Name | Value | Units | Value in previous GBL models [1] [2] | Remarks-Reference |
|---|---|---|---|---|
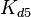
|
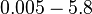 [3] [4] [5] [6] [3] [4] [5] [6]
|
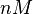
|
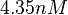
(Range tested: (Bistability range: |
An early publication based on stopped-flow measurements at various salt concentrations reports a KA of 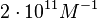 [3], therefore a Kd ( [3], therefore a Kd (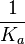 ) of ) of 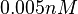 . The Tet repressor and TetO operator were derived by using an overproducing E. coli strain. . The Tet repressor and TetO operator were derived by using an overproducing E. coli strain.
 Kleinschmidt et al. 1988[3] Data derived from equilibrium SPR analysis of TetR-tetO interaction report a Ka of 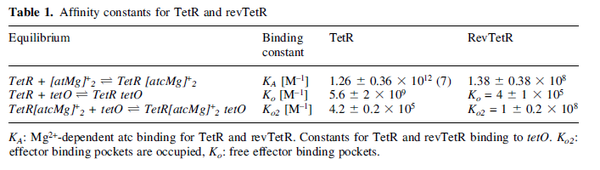 Kamionka et al. 2004 [4] Additionally, a study on the TetR-like protein Rv3066 binding to the mmr operon in M. tuberculosis suggests a Kd of  Bolla et al. 2012 [5] Finally, in vitro studies on TetR-like protein ActR in S. coelicolor suggest a Kd in the range of  Ahn et al. 2007 [6] |
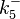
|
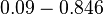 [3] [7] [3] [7]
|
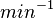
|
N/A | According to the study by Kleinschmidt et al.[3] mentioned above, the maximal association rate constant was 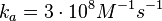 . By taking into account the equilibrium association constant reported above ( . By taking into account the equilibrium association constant reported above (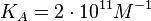 ), the dissociation rate constant can be calculated as per ), the dissociation rate constant can be calculated as per 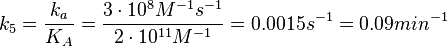 . .
 Kleinschmidt et al. 1988[3] Additionally, a study on a TetR-like protein (RolR) which binds to its operator rolO and blocks the transcription of rolHMD and of its own gene, in Corynebacterium glutamicum (Gram positive and GC content ~ 50-60% bacteria) reports the dissociation rates 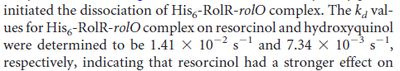 Li et al. 2012[7] As less information was available for |
Parameters with uncertainty
When deciding how to describe the uncertainty for each parameter there are a few points to be taken into consideration. Firstly, the values reported in literature are spread in a relatively large range and correspond to different protein-operator binding reactions, although all are part of the same family of repressors (TetR). Additionally, the values were acquired by in vitro testing, although in some of the publications a strong correlation between in vitro and in vivo measurements is noted. This means that there might be a notable difference between actual parameter values and the ones reported in literature. These facts influence the weight assigned to each parameter value, the quantification of the parameter uncertainty and therefore the shape of the corresponding distributions. Therefore, by assigning the appropriate weights to the parameter values and using the method described here, the appropriate probability distributions were designed.
More specifically, with regards to the 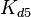 , the value that is considered as the most accurate in different publications is
, the value that is considered as the most accurate in different publications is 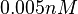 measured by Kleinschmidt et al. However, the Kd s measured for the ActR protein in S. coelicolor cover the range of
measured by Kleinschmidt et al. However, the Kd s measured for the ActR protein in S. coelicolor cover the range of 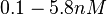 . Therefore, the mode of the log-normal distribution calculated for the
. Therefore, the mode of the log-normal distribution calculated for the 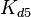 is
is 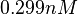 which is within the range of the values reported for S. coelicolor and the Spread is
which is within the range of the values reported for S. coelicolor and the Spread is 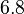 in order to be able to explore a wide range of values and thus take into account the uncertainty caused by both the in vitro testing and the measurements in different species and proteins. Thus, the range where 68.27% of the values are found is between 0.044 and 2.048 nM.
in order to be able to explore a wide range of values and thus take into account the uncertainty caused by both the in vitro testing and the measurements in different species and proteins. Thus, the range where 68.27% of the values are found is between 0.044 and 2.048 nM.
Similarly, the value calculated for the 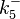 by the measurements of Kleinschmidt et al. is
by the measurements of Kleinschmidt et al. is 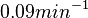 , however other studies reported values of up to
, however other studies reported values of up to 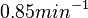 . After considering all the factors and assigning the relevant weights to the parameter values, the mode of the log-normal distribution calculated for
. After considering all the factors and assigning the relevant weights to the parameter values, the mode of the log-normal distribution calculated for 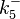 was
was 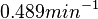 and the Spread was
and the Spread was 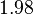 . This means that the range where 68.27% of the values are found is between 0.247 and 0.968
. This means that the range where 68.27% of the values are found is between 0.247 and 0.968 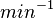 .
.
Since the two parameters are interdependent, thermodynamic consistency also needs to be taken into account. This is achieved by creating a bivariate system as described here. Since 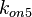 is the parameter with the largest geometric coefficient of variation, as only one reported value was retrieved from literature, this is set as the dependent parameter as per:
is the parameter with the largest geometric coefficient of variation, as only one reported value was retrieved from literature, this is set as the dependent parameter as per: 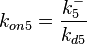 . The location and scale parameters of
. The location and scale parameters of 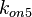 (μ=-0.53113 and σ=1.3034) were calculated from those of
(μ=-0.53113 and σ=1.3034) were calculated from those of 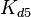 and
and 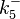 .
.
The probability distributions for the three parameters, adjusted accordingly in order to reflect the above values, are the following:
The values retrieved from literature and their weights are indicated by the blue dashed lines, and the uncertainty for each value is indicated using the reported experimental error (green lines) or a default value of 10% error (orange lines). The correlation matrix which is necessary to define the relationship between the two marginal distributions (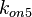 ,
,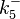 ) of the bivariate system is derived by employing random values generated by the two distributions.
) of the bivariate system is derived by employing random values generated by the two distributions.
The parameter information of the distributions of the multivariate system is:
| Parameter | Mode | Spread | μ | σ | Correlation matrix |
|---|---|---|---|---|---|
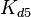
|
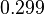
|
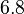
|
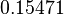
|
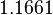
|
N/A |
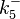
|
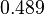
|
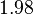
|
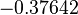
|
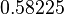
|
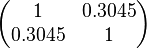
|
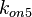
|
N/A | N/A | 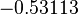
|
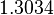
|
The multivariate system of the normal distributions (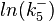 and
and 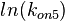 ) and the resulting samples of values are presented in the following figure:
) and the resulting samples of values are presented in the following figure:
In this way, a system of distributions is created where each distribution is described and constrained by the other two. Therefore, the parameters will be sampled by the two marginal distributions in a way consistent with our beliefs and with the relevant thermodynamic constraints. However, since the model's reaction rate requires the parameters 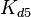 and
and 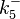 , and not the
, and not the 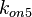 , the value for
, the value for 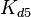 is calculated by the parameters sampled from the other two distributions in an additional step, as per
is calculated by the parameters sampled from the other two distributions in an additional step, as per 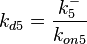 .
All the above apply as well for the parameters
.
All the above apply as well for the parameters 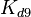 ,
, 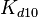 ,
, 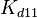 ,
, 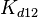 ,
, 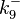 ,
, 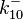 ,
, 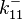 and
and 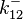 .
.
References
- ↑ S. Mehra, S. Charaniya, E. Takano, and W.-S. Hu. A bistable gene switch for antibiotic biosynthesis: The butyrolactone regulon in streptomyces coelicolor. PLoS ONE, 3(7), 2008.
- ↑ A. Chatterjee, L. Drews, S. Mehra, E. Takano, Y.N. Kaznessis, and W.-S. Hu. Convergent transcription in the butyrolactone regulon in streptomyces coelicolor confers a bistable genetic switch for antibiotic biosynthesis. PLoS ONE, 6(7), 2011.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Kleinschmidt C., Tovar K., Hillen W., Porschke D. Dynamics of repressor-operator recognition: Tn10-encoded tetracycline resistance control. Biochemistry, 1988, 27(4), pp. 1094–1104.
- ↑ 4.0 4.1 4.2 Kamionka A, Bogdanska-Urbaniak J, Scholz O, Hillen W. Two mutations in the tetracycline repressor change the inducer anhydrotetracycline to a corepressor. Nucleic Acids Research. 2004;32(2):842-847.
- ↑ 5.0 5.1 5.2 Bolla JR, Do SV, Long F, et al. Structural and functional analysis of the transcriptional regulator Rv3066 of Mycobacterium tuberculosis. Nucleic Acids Research. 2012;40(18):9340-9355.
- ↑ 6.0 6.1 6.2 Ahn SK, Tahlan K, Yu Z, Nodwell J. Investigation of Transcription Repression and Small-Molecule Responsiveness by TetR-Like Transcription Factors Using a Heterologous Escherichia coli-Based Assay. Journal of Bacteriology. 2007;189(18):6655-6664.
- ↑ 7.0 7.1 7.2 Li T, Zhao K, Huang Y, et al. The TetR-Type Transcriptional Repressor RolR from Corynebacterium glutamicum Regulates Resorcinol Catabolism by Binding to a Unique Operator, rolO. Applied and Environmental Microbiology. 2012;78(17):6009-6016.


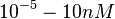 )
)
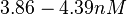 )
)
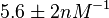
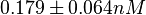 . E. coli was used as a host for the expression of proteins and the experiments were conducted with synthetic tetO-containing fragments.
. E. coli was used as a host for the expression of proteins and the experiments were conducted with synthetic tetO-containing fragments.
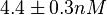 .
.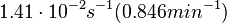 and
and